一、单选题 (共 26 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设 $X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的简单随机样本, 其中 $P(X=0)=P(X=1)=\frac{1}{2}, \Phi(x)$ 表 示标准正态分布函数, 则利用中心极限定理可得 $P\left(\sum_{i=1}^{100} X_i \leq 55\right)$ 的近似值为
$\text{A.}$ $1-\Phi(1)$
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $1-\Phi(2)$
$\text{D.}$ $\Phi(2)$
设随机事件 $A, B, C$ 两两相互独立且满足条件 $P(A B C)=0, P(A)=P(B)=P(C) < $ $\frac{1}{2}, P(A \cup B \cup C)=\frac{9}{16}$, 则 $P(A)$
$\text{A.}$ $\frac{3}{4}$
$\text{B.}$ $\frac{3}{8}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{1}{4}$
设 $X_1, X_2, \cdots, X_n(n \geqslant 2)$ 是来自总体 $N\left(0, \sigma^2\right)$ 的简单随机样本, 令 $\alpha=\sum_{i=1}^n X_i, \beta=\sum_{i=1}^n X_i^2$, 则下列说法中错误的是
$\text{A.}$ $\frac{\alpha^2}{n \sigma^2}$ 服从 $\chi^2$ 分布
$\text{B.}$ $\frac{\beta}{\sigma^2}$ 服从 $\chi^2$ 分布
$\text{C.}$ $\frac{\alpha^2}{\beta}$ 服从 $F$ 分布
$\text{D.}$ $\frac{\left(X_1-X_2\right)^2}{\left(X_1+X_2\right)^2}$ 服从 $F$ 分布
设连续型随机变量 $X_1, X_2$ 的概率密度分别为 $f_1(x), f_2(x)$, 其分布函数分别为 $F_1(x), F_2(x)$, 记 $g_1(x)=f_1(x) F_2(x)+f_2(x) F_1(x), g_2(x)=f_1(x) F_1(x)+f_2(x) F_2(x), g_3(x)=$ $\frac{1}{2}\left[f_1(x)+f_2(x)\right], g_4(x)=\sqrt{f_1(x) f_2(x)}$, 则 $g_1(x), g_2(x), g_3(x), g_4(x)$ 这 4 个函数中一定 能作为概率密度的共有
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设随机变量 $X, Y$ 相互独立, 且 $X \sim E(a), Y \sim E(b)(a>0, b>0, a \neq b)$, 则服从 $E(a+b)$ 的 随机变量是
$\text{A.}$ $X+Y$.
$\text{B.}$ $X Y$.
$\text{C.}$ $\max \{X, Y\}$.
$\text{D.}$ $\min \{X, Y\}$.
设 $X_1, X_2, \cdots, X_{10}$ 为来自总体 $X$ 的简单随机样本, $E(X)$ 与 $D(X)$ 都存在, 且 $\bar{X}=\frac{1}{10} \sum_{i=1}^{10} X_i$, 若 $E\left(X_1 \bar{X}\right)=35, D\left(X_1-\bar{X}\right)=90$, 则 $E\left(X^2\right)=$
$\text{A.}$ 100
$\text{B.}$ 125
$\text{C.}$ 150
$\text{D.}$ 175
设 $X_1, X_2, X_3, X_4$ 为来自总体 $N\left(1, \sigma^2\right)(\sigma>0)$ 的简单随机样本, $\bar{X}$ 为样本均值, $S^2$ 为样本方差, 则下列选项正确的是
$\text{A.}$ $\frac{X_1-X_2}{\left|X_3+X_4-2\right|} \sim t(2)$.
$\text{B.}$ $\frac{4(\bar{X}-1)^2}{\sigma^2} \sim \chi^2(2)$.
$\text{C.}$ $\frac{4(\bar{X}-1)^2}{S^2} \sim F(3,1)$.
$\text{D.}$ $\frac{\left(X_1-X_2\right)^2+\left(X_3-X_4\right)^2}{2 \sigma^2} \sim E\left(\frac{1}{2}\right)$.
已知 $X \sim N(0,4)$, 样本 $X_1, X_2$ 取自总体 $X$, 则统计量 $T=\frac{\left(X_1-X_2\right)^2}{\left(X_1+X_2\right)^2}$ 服从的分布是
$\text{A.}$ $F(1,1)$.
$\text{B.}$ $\chi^2(1)$.
$\text{C.}$ $N(0,1)$.
$\text{D.}$ $t(1)$.
设随机变量 $X$ 与 $Y$ 相互独立, 且 $X \sim N(0,1)$,
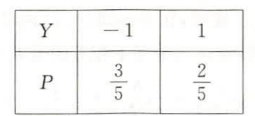
令随机变量 $Z=X Y$, 则 $Z$ 的分布为
$\text{A.}$ $N(-1,1)$.
$\text{B.}$ 与 $Y$ 同分布.
$\text{C.}$ $N(0,1)$.
$\text{D.}$ $N\left(\frac{1}{3}, \frac{2}{3}\right)$.
下面的函数中可以是离散型随机变量的概率函数
$\text{A.}$ $P\left\{\xi_1=k\right\}=\frac{e^{-1}}{k !}(k=0,1,2 \| 1)$
$\text{B.}$ $P\left\{\xi_2=k\right\}=\frac{e^{-1}}{k !}(k=1,2\|\|)$
$\text{C.}$ $P\left\{\xi_3=k\right\}=\frac{1}{2^k}(k=0,1,2 \|)$
$\text{D.}$ $P\left\{\xi_4=k\right\}=\frac{1}{2^k}(k=-1,-2,-3\|\|)$
设 $F_1(x)$ 与 $F_2(x)$ 分别为随机变量 $X_1$ 与 $X_2$ 的分布函数, 为了使 $F(x)=a F_1(x)-b F_2(x)$ 是某一随机变量的分布函数, 则下列个组中应取
$\text{A.}$ $a=-\frac{1}{2}, b=\frac{3}{2}$
$\text{B.}$ $a=\frac{2}{3}, b=\frac{2}{3}$
$\text{C.}$ $a=\frac{3}{5}, b=-\frac{2}{5}$
$\text{D.}$ $a=\frac{1}{2}, b=-\frac{3}{2}$
在进行一元线性回归时, 通过最小二乘法求得的经验回归系数 $\hat{b}$ 为 $\frac{l_{x y}}{l_{x x}} $
$\text{A.}$ 正确
$\text{B.}$ 错误
$\text{C.}$
$\text{D.}$
设某次考试考生的成绩服从正态分布 $N\left(70, \sigma^2\right), \sigma^2$ 末知, 为了检验样本均值是 否显著改变, 抽取 36 名同学测得平均成绩为 $66.5$ 分, 标准差为 15 分, 显著水平 $\alpha=0.05$, 则应该接受原假设。
$\text{A.}$ 正确
$\text{B.}$ 错误
$\text{C.}$
$\text{D.}$
$X \sim N\left(\mu, 4^2\right), Y \sim N\left(\mu, 5^2\right), p_1=P\{X \leq \mu-4\}, p_2=P\{Y \geq \mu+5\}$, 则
$\text{A.}$ 对任意实数 $\mu, p_1=p_2$
$\text{B.}$ 对任意实数 $\mu, p_1 < p_2$
$\text{C.}$ 只对 $\mu$ 的个别值, 才有 $p_1=p_2$
$\text{D.}$ 对任意实数 $\mu$, 都有 $p_1>p_2$
设随机变量 $X$ 的密度函数为 $f(x)$, 且 $f(-x)=f(x), F(x)$ 是 $X$ 的分布函数, 则对任 意 实数 $a$ 成立的是 ( )
$\text{A.}$ $F(-a)=1-\int_0^a f(x) d x$
$\text{B.}$ $F(-a)=\frac{1}{2}-\int_0^a f(x) d x$
$\text{C.}$ $F(-a)=F(a)$
$\text{D.}$ $F(-a)=2 F(a)-1$
设二维随机变量 $(X, Y) \sim N(0,0 ; 1,1 ; 0), U=a X+b Y, V=c X+d Y$, 其中 $a, b, c, d$ 为实 数, 则 $(U, V) \sim N(0,0 ; 1,1 ; 0)$ 是 $\left(\begin{array}{cc}a & b \\ c & d\end{array}\right)$ 为正交矩阵的
$\text{A.}$ 充分必要条件
$\text{B.}$ 充分非必要条件
$\text{C.}$ 必要非充分条件
$\text{D.}$ 非充分非必要条件
设随机变量 $X$ 和 $Y$ 相互独立同分布, 若 $P(X>1)=p$, 则 $P(\max (X, Y)>1)=$
$\text{A.}$ $p$
$\text{B.}$ $1-(1-p)^2$
$\text{C.}$ $(1-p)^2$
$\text{D.}$ $p^2$
从总体 $X \sim N\left(\mu, \sigma^2\right)$ 中抽取容量 $\boldsymbol{n}$ 的一个样本, 样本均值为 $\bar{X}$, 样本方差为 $S^2$, 下面错 误的是
$\text{A.}$ $E\left(\frac{(n-1) S^2}{\sigma^2}\right)=n-1$
$\text{B.}$ $D\left(S^2\right)=\frac{2 \sigma^4}{n}$
$\text{C.}$ $D\left(\left(\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}\right)^2\right)=2$
$\text{D.}$ $E\left(n S^2\right)=n \sigma^2$
设总体 $X \sim N(0,1)$, 样本 $X_1, X_2, \cdots, X_n(n>1)$ 为来自该总体的简单随机样本, $\bar{X}$ 与 $S$ 分 别为样本均值和样本标准差, 则有
$\text{A.}$ $\bar{X} \sim N(0,1)$
$\text{B.}$ $n \bar{X} \sim N(0,1)$
$\text{C.}$ $\frac{\sqrt{n} \bar{X}}{S} \sim t(n-1)$
$\text{D.}$ $\frac{n \bar{X}}{S} \sim t(n-1)$
设总体 $X$ 的均值及方差都存在, 从中抽取样本 $X_1, X_2, \cdots, X_n(n \geq 3)$, 下面总体均值的最 有效的无偏估计是
$\text{A.}$ $\left(3 X_1+X_2+X_3\right) / 5$
$\text{B.}$ $\left(X_1+X_2+X_3\right) / 3$
$\text{C.}$ $\left(X_1+X_2\right) / 2$
$\text{D.}$ $X_2$
从总体 $X \sim N\left(\mu, \sigma^2\right)$ ( $\mu, \sigma^2$ 均末知)中抽取容量 $\boldsymbol{n}$ 的一个样本, 样本均值为 $\bar{X}$, 样本方 差为 $S^2$, 则 $\mu$ 的置信度为 $90 \%$ 的双侧置信区间是
$\text{A.}$ $\left(\bar{X} \mp \frac{\sigma}{\sqrt{n}} z_{0.05}\right)$
$\text{B.}$ $\left(\bar{X} \mp \frac{\sigma}{\sqrt{n}} z_{0.1}\right)$
$\text{C.}$ $\left(\bar{X} \mp \frac{S}{\sqrt{n}} t_{0.05}(n-1)\right)$
$\text{D.}$ $\left(\bar{X} \mp \frac{S}{\sqrt{n}} t_{0.1}(n-1)\right)$
设随机事件 $A, B, C$ 两两独立, 且 $P(A)=P(B)=\frac{1}{2}, P(C)=\frac{1}{3}, P(A B \mid C)=\frac{1}{3}$, 则在 $A$ 不发生的条件下 $B$ 与 $C$ 都发生的概率是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{1}{9}$
设随机变量 $\mathrm{X}$ 的概率密度为 $\boldsymbol{p}(\boldsymbol{x})=\left\{\begin{array}{l}\boldsymbol{c} \quad 1 < x < 3 \\ \mathbf{0}, \quad \text { 其他 }\end{array}\right.$ 则方差 $\mathrm{D}(\mathrm{X})=$
$\text{A.}$ $2$
$\text{B.}$ $\frac{1}{2}$;
$\text{C.}$ $3$
$\text{D.}$ $\frac{1}{3}$.
设 $A 、 B$ 为两个互不相容的随机事件, 且 $P(B)>0$, 则下列选项必然正确的是
$\text{A.}$ $P(A)=1-P(B)$
$\text{B.}$ $P(A \mid B)=0 $
$\text{C.}$ $P(A \mid B)=1$
$\text{D.}$ $P(\overline{A B})=0$
设 $f(x)=\sin x$ 是某个连续型随机变量 $X$ 的概率密度函数, 则 $X$ 的取值范围是
$\text{A.}$ $\left[0, \frac{\pi}{2}\right]$
$\text{B.}$ $[0, \quad \pi]$
$\text{C.}$ $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
$\text{D.}$ $\left[\pi, \frac{3 \pi}{2}\right]$
设 $X \sim N\left(\mu, \sigma^2\right), Y=a X-b$, 其中 $a 、 b$ 为常数, 且 $a \neq 0$, 则 $Y \sim$
$\text{A.}$ $N\left(a \mu-b, \quad a^2 \sigma^2+b^2\right)$;
$\text{B.}$ $N\left(a \mu+b, \quad a^2 \sigma^2-b^2\right)$;
$\text{C.}$ $N\left(a \mu+b, \quad a^2 \sigma^2\right)$
$\text{D.}$ $N\left(a \mu-b, \quad a^2 \sigma^2\right)$
二、填空题 (共 17 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设随机变量 $X$ 和 $Y$ 相互独立, $X$ 服从参数为 1 的指数分布, $Y$ 的分布为 $\mathbb{P}(Y=1)=$ $\frac{1}{4}, \mathbb{P}(Y=2)=\frac{3}{4}$, 则 $\mathbb{P}(1 \leqslant \min \{X, Y\} < 2)=$
设随机变量 $X_1, X_2, \cdots, X_9$ 独立同分布, 其方差为 $\sigma^2(\sigma>0)$, 又设 $U=\sum_{i=1}^7 X_i, V=\sum_{i=3}^9 X_i$, 则 $U$ 与 $V$ 的相关系数 $\rho_{U V}=$
已知某产品的生产函数为 $Q=A K^\alpha L^\beta$, 其中 $Q$ 为产量, $K$ 表示资金, $L$ 表示劳力, $A, \alpha, \beta$ 为正常数, 且 $\alpha+\beta=1$, 则 $K \frac{\partial Q}{\partial K}+L \frac{\partial Q}{\partial L}=$
一个口袋中有 3 个白球、 5 个黑球, 每次从中取一球, 且取后放回, 重复抽取 $n$ 次. 已知在取白球 $k$ 次的条件下, 事件 $B$ 发生的概率为 $\frac{k}{n}$, 则 $P(B)=$
设随机变量序列 $X_1, X_2, \cdots, X_n, \cdots$ 相互独立, 且都服从 $\lambda=\frac{1}{2}$ 的指数分布, $\Phi(x)$ 是标准正态 分布的分布函数, 则 $\lim _{n \rightarrow \infty} P\left\{\sum_{i=1}^n X_i \leqslant 2 n+2 \sqrt{n}\right\}=$
设平面区域 $G$ 是由直线 $y=0, x=\mathrm{e}$ 以及曲线 $y=\ln x$ 围成, 随机变量 $(X, Y)$ 在区域 $G$ 内服 从均匀分布.
(I) 求条件密度函数 $f_{X \mid Y}(x \mid y)$ 与 $f_{Y \mid X}(y \mid x)$;
(II) $F(x, y)$ 是 $(X, Y)$ 的分布函数,求 $F\left(\frac{\mathrm{e}}{2}, \ln \frac{\mathrm{e}}{2}\right)$;
(III) 设 $\left(Y_1, Y_2, \cdots, Y_n\right)$ 是取自 $Y$ 的样本, $S^2=\frac{1}{n-1} \sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2$ 为样本方差, 求 $E\left(S^2\right)$.
设 $(\xi, \eta)$ 的联合分布律如表所示, 则 $(\mathrm{a}, \mathrm{b})=(\quad)$ 时, $\xi$ 与 $\eta$ 相互独立。
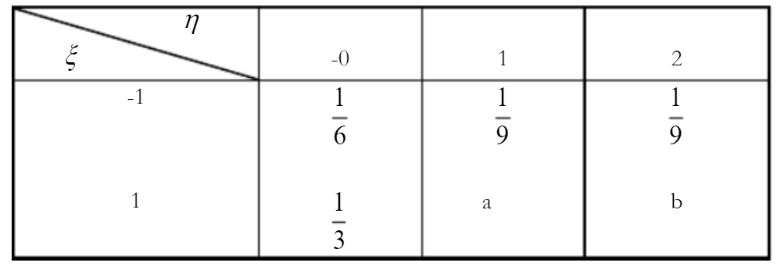
设 $x_1, \cdots, x_6$ 为正态总体 $N\left(0,2^2\right)$ 的一个样本, 则概率 $P\left\{\sum_{i=1} ^6x_i^2>6.54\right\}$ 为
设随机变量 $\xi$ 的概率密度为 $f(x)=\left\{\begin{array}{cc}k x^b & 0 < x < 1,(b>0, k>0) \\ 0 & \text { 其他 }\end{array}\right.$ 且 $P\left(\xi>\frac{1}{2}\right)=0.75$, 则 $\mathrm{K}$ 和 $\mathrm{b}$ 分别为多少?
设随机变量 $X$ 有密度 $f(x)=\left\{\begin{array}{lr}4 x^3, & 0 < x < 1 \\ 0 & \text { 其它 }\end{array}\right.$, 则使 $P(X>a)=P(X < a)$ 的常数 $a=$
设随机变量 $X \sim N\left(2, \sigma^2\right)$, 若 $P\{0 < X < 4\}=0.3$, 则 $P\{X < 0\}=$
设 $f(x)=\frac{1}{\sqrt{\pi}} e^{-x^2+2 x-1}$, 则 $E X=$
设随机变量 $X$ 和 $Y$ 相互独立, $X \sim B\left(1, \frac{1}{2}\right), Y \sim P(1), Z=\left\{\begin{array}{l}0, X=0, \\ Y, X=1,\end{array}\right.$ 则 $X$ 与 $Z$ 的相关
系数为
某元件寿命 $X$ (单位: 小时) 服从 $[100,120]$ 上的均匀分布, 若选取 $n$ 只独立元件寿命分别为 $X_1, \ldots, X_n$, 以 $Y_n$ 表示 $n$ 只元件中寿命超过 110 小时的元件数, 则 $Y_n$ 服从 分
布; 当 $n \rightarrow+\infty$ 时, 由大数定理知, $\frac{Y_n}{n}$ 依概率收敛于 ; $n$ 足够大时, 由中心 极限定理得 $\sum_{i=1}^n X_i$ 近似服从 ,而 $\frac{1}{n} \sum_{i=1}^n X_i$ 近似服从