单选题 (共 6 题 ),每题只有一个选项正确
已知随机变量 $\boldsymbol{X}$ 服从二项分布,且$E(X)=2.4, \quad D(X)=1.44 $ 则二项分布的参数 $n, p$ 的值为
$\text{A.}$ $n=4, \quad p=0.6$
$\text{B.}$ $n=6, \quad p=0.4$
$\text{C.}$ $n=8, \quad p=0.3$
$\text{D.}$ $n=24, \quad p=0.1$
设随机变量 $\boldsymbol{X}$ 和 $Y$ 相互独立,其概率分布为
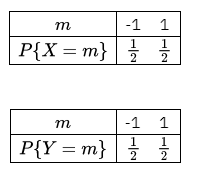
则下列式子正确的是
$\text{A.}$ $X=Y$
$\text{B.}$ $P\{X=Y\}=0$
$\text{C.}$ $P\{X=Y\}=\frac{1}{2}$
$\text{D.}$ $P\{X=Y\}=1$
对任意两随机变量 $X$ 和 $Y$ ,若 $E(X Y)=E(X) \cdot E(Y)$ ,则
$\text{A.}$ $D(X Y)=D(X) \cdot D(Y)$
$\text{B.}$ $D(X+Y)=D(X)+D(Y)$
$\text{C.}$ ${X}$ 和 ${Y}$ 独立
$\text{D.}$ $X$ 和 $Y$ 不独立
设 $F_1(x) , F_2(x)$ 为两个分布函数,其相应的概率密度 $f_1(x)$ , $f_2(x)$ 是连续函数,则必为概率密度的是
$\text{A.}$ $f_1(x) f_2(x)$
$\text{B.}$ $2 f_2(x) F_1(x)$
$\text{C.}$ $f_1(x) F_2(x)$
$\text{D.}$ $f_1(x) F_2(x)+f_2(x) F_1(x)$
设随机变量 $X$ 与 $Y$ 相互独立,且分别服从参数为 1 与参数为 4 的指数分布,则 $P\{X < Y\}=(\quad)$
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{4}{5}$
将长度为 1 m 的木棒随机地截成两段,则两段长度的相关系数为
$\text{A.}$ 1
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ -1