一、单选题 （共 53 题，每小题 5 分，共 50 分，每题只有一个选项正确）
已知正四棱锥的侧棱长为 1 , 其各顶点都仕同一球面上. 若该球的体积为 $36 \pi$, 且 $3 \leqslant 1 \leqslant 3 \sqrt{3}$, 则该正四棱雉体积的取值范围是
$\text{A.}$ $\left[18, \frac{81}{4}\right]$
$\text{B.}$ $\left[\frac{27}{4}, \frac{81}{4}\right]$
$\text{C.}$ $\left[\frac{27}{4}, \frac{64}{3}\right]$
$\text{D.}$ $[18,27]$
已知 $a=3^{0.2}, b=\log _{6} 7, c=\log _{5} 6$, 则
$\text{A.}$ $a>b>c$
$\text{B.}$ $b>c>a$
$\text{C.}$ $a>c>b$
$\text{D.}$ $b>a>c$
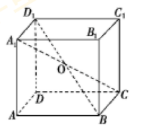
如图, 已知正方体 $A B C D-A_{1} B_{1} C_{1} D_{1}$ 的中心为 $O$, 则下列结论中
1. $\overrightarrow{O A}+\overrightarrow{O D}$ 与 $\overrightarrow{O A}_{1}+\overrightarrow{O D}_{1}$ 是一对相反向量;
2.$\overrightarrow{O B}-\overrightarrow{O C}_{1}$ 与 $\overrightarrow{O C}-\overrightarrow{O B}_{1}$ 是一对相反向量;
3.$\overrightarrow{O A}_{1}+\overrightarrow{O B}_{1}+\overrightarrow{O C}_{1}+\overrightarrow{O D}_{1}$ 与 $\overrightarrow{O D}+\overrightarrow{O C}+\overrightarrow{O B}+\overrightarrow{O A}$ 是一对相反向量;
4.$\overrightarrow{O C}-\overrightarrow{O A}$ 与 $\overrightarrow{O C}_{1}-\overrightarrow{O A}_{1}$ 是一对相反向量.
正确结论的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知平面向量 $\vec{a}, \vec{b}, \vec{c}$ 满足 $|\vec{a}|=|\vec{b}|=\vec{a} \cdot \vec{b}=2$, 且 $(\vec{b}-\vec{c}) \cdot(3 \vec{b}-\vec{c})=0$, 则 $|\vec{c}-\vec{a}|$ 最小值 为
$\text{A.}$ $2 \sqrt{2}+1$
$\text{B.}$ $3 \sqrt{3}-3$
$\text{C.}$ $\sqrt{7}-1$
$\text{D.}$ $2 \sqrt{3}-2$
已知函数 $f(x)=\left\{\begin{array}{c}\left(\frac{1}{3}\right)^{x}, x \leqslant 0, \\ \log _{3} x-2, x>0,\end{array}\right.$ 则 $f(f(-3))$ 的值为
$\text{A.}$ $-3$
$\text{B.}$ $-2$
$\text{C.}$ 0
$\text{D.}$ 1
已知函数 $y=a^{x+4}+2(a>0$, 且 $a \neq 1)$ 的图象恒过点 $P$, 若角 $\alpha$ 的终边经过点 $P$, 则 $\cos \alpha$ 的值为
$\text{A.}$ $-\frac{4}{5}$
$\text{B.}$ $-\frac{2 \sqrt{2}}{3}$
$\text{C.}$ $\frac{\sqrt{2}}{3}$
$\text{D.}$ $\frac{3}{5}$
如图的曲线就像横放的葫芦的轴截面的边缘线, 我们叫葫芦曲线(也像湖面上高低起伏 的小岛在水中的倒影与自身形成的图形, 也可以形象地称它为倒影曲线), 它对应的方程为$|y|=\left(3-\frac{1}{3}\left[\frac{3 x}{\pi}\right]\right) \cdot|\sin \omega x|(0 \leqslant x \leqslant 3 \pi)$ (其中记 $[x]$ 为不超过 $x$ 的最大整数), 且过点 $P\left(\frac{\pi}{6}, 3\right)$, 若 葫芦曲线上一点 $M$ 到 $y$ 轴的距离为 $\frac{17 \pi}{6}$, 则点 $M$ 到 $x$ 轴的距离为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
若棱长为 $2 \sqrt{3}$ 的正方体的顶点都在同一球面上, 则该球的表面积为 ( )
$\text{A.}$ $12 \pi$
$\text{B.}$ $24 \pi$
$\text{C.}$ $36 \pi$
$\text{D.}$ $144 \pi$
已知函数 $f(x)=\left\{\begin{array}{ll}x^{3}, & x . .0, \\ -x, & x < 0 .\end{array}\right.$ 若函数 $g(x)=f(x)-\left|k x^{2}-2 x\right| \quad(k \in \mathbf{R})$ 恰有 4 个零点, 则 $k$ 的取值范围 是 ( )
$\text{A.}$ $\left(-\infty,-\frac{1}{2}\right) \cup(2 \sqrt{2},+\infty)$
$\text{B.}$ $\left(-\infty,-\frac{1}{2}\right) \cup(0,2 \sqrt{2})$
$\text{C.}$ $(-\infty, 0) \cup(0,2 \sqrt{2})$
$\text{D.}$ $(-\infty, 0) \cup(2 \sqrt{2},+\infty)$
函数 $f(x)=\ln x-x$ 在 $(0, e]$ 上的最大值为
$\text{A.}$ $-1$
$\text{B.}$ 1
$\text{C.}$ $1-e$
$\text{D.}$ $e$
若函数 $f(x)=k x+\ln x$ 在区间 $(1 ， 3)$ 上单调递增，则实数 $k$ 的取值范围是
$\text{A.}$ $[-1,+\infty)$
$\text{B.}$ $\left[-\frac{1}{6},+\infty\right)$
$\text{C.}$ $\left[-\frac{1}{3},+\infty\right)$
$\text{D.}$ $(-\infty,-1]$
祖晅是我国南北朝时代的伟大科学家. 他提出的 “幂势既同, 则积不容易” 称为祖㫜原理, 利用该原理可以得到柱体体积公式 $V$ 梇伡 $=S h$, 其中 $S$ 是柱体的底面积, $h$ 是柱体的高. 若某 柱体的三视图如图所示, 则该柱体的体积是
$\text{A.}$ 158
$\text{B.}$ 162
$\text{C.}$ 182
$\text{D.}$ 32
设三棱雉 $V-A B C$ 的底面是正三角形, 侧棱长均相等, $P$ 是棱 $V A$ 上的点 (不含端点), 记直 线 $P B$ 与直线 $A C$ 所成角为 $\alpha$, 直线 $P B$ 与平面 $A B C$ 所成角为 $\beta$, 二面角 $P-A C-B$ 的平面角 为 $\gamma$, 则
$\text{A.}$ $\beta < \gamma, \quad \alpha < \gamma$
$\text{B.}$ $\beta < \alpha, \beta < \gamma$
$\text{C.}$ $\beta < \alpha, \gamma < \alpha$
$\text{D.}$ $\alpha < \beta, \gamma < \beta$
已知向量 $\vec{a}, \vec{b}$, 的夹角为 $\frac{\pi}{3}$, 且 $|\vec{a}|=2,|\vec{b}|=3$, 则 $\vec{a} \cdot(\vec{b}-\vec{a})=($ )
$\text{A.}$ $-1$
$\text{B.}$ $3 \sqrt{3}-4$
$\text{C.}$ $-2$
$\text{D.}$ 1
下列四个向量中, 与向量 $a=(-2,3)$ 共线的是
$\text{A.}$ $(3,2)$
$\text{B.}$ $(3,-2)$
$\text{C.}$ $(4,-6)$
$\text{D.}$ $(4,6)$
已知 $F_{1}, F_{2}$ 分别是椭圆 $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左、右焦点, 点 $P, Q$ 是 $C$ 上位于 $x$ 轴上方 的任意两点, 且 $P F_{1} / / Q F_{2}$. 若 $\left|P F_{1}\right|+\left|Q F_{2}\right| \geqslant b$, 则 $C$ 的离心率的取值范围是
$\text{A.}$ $\left(0, \frac{1}{2}\right]$
$\text{B.}$ $\left[\frac{1}{2}, 1\right)$
$\text{C.}$ $\left(0, \frac{\sqrt{3}}{2}\right]$
$\text{D.}$ $\left[\frac{\sqrt{3}}{2}, 1\right)$
不等式 $(1+x)(2-x)>0$ 的解集为
$\text{A.}$ $(-\infty,-1) \cup(2,+\infty)$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $(-\infty,-2) \cup(1,+\infty)$
$\text{D.}$ $(-2,1)$
若 $a 、 b 、 c$ 是常数, 则 “ $a>0$ 且 $b^{2}-4 a c < 0$ ”是 “对任意 $x \in R$, 有 $a x^{2}+b x+c>0$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 即不充分也不必要条件
设集合 $M=\{x \in N \mid y=\lg (3-x)\}, N=\left\{y \mid y=2^x, x \in M\right\}$, 则
$\text{A.}$ $M \subseteq N$
$\text{B.}$ $N \subseteq M$
$\text{C.}$ $M \cap N=\{0,1,2\}$
$\text{D.}$ $M \cup N=\{0,1,2,4\}$
命题 “存在实数 $x_0$, 使 $e^{x_0}>\frac{1}{x_0}$ ” 的否定是
$\text{A.}$ 不存在实数 $x_0$, 使 $e^{x_0} \leq \frac{1}{x_0}$
$\text{B.}$ 存在实数 $x_0$, 使 $e^{x_0} \leq \frac{1}{x_0}$
$\text{C.}$ 对任意的实数 $x$, 都有 $e^x \leq \frac{1}{x}$
$\text{D.}$ 对任意的实数 $x$, 都有 $e^x>\frac{1}{x}$
已知 $F$ 为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的另焦点, $A$ 为 $C$ 的左顶点, $B$ 为 $C$ 上 的点, 且 $B F$ 垂直于 $ x$ 轴, 若直线 $A B$的倾角为$\frac{\pi}{4} $,则双曲线 $C$ 的离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ 2
$\text{D.}$ 3
双曲函数在实际生活中有着非常重要的应用, 比如悬链桥. 在数学中, 双曲函数是一 类与三角函数类似的函数, 最基础的是双曲正弦函数 $\sinh x=\frac{e^x-e^{-x}}{2}$ 和双曲余弦函数 $\cosh x=\frac{e^x+e^{-x}}{2}$. 下列结论错误的是
$\text{A.}$ 双曲正弦函数图象关于原点中心对称, 双曲余弦函数图象关于 $y$ 轴对称
$\text{B.}$ 若直线 $y=m$ 与双曲余弦函数图象 $C_1$ 和双曲正弦函数图象 $C_2$ 共有三个交点, 则 $m \geq 1$
$\text{C.}$ 双曲余弦函数图象 $C_1$ 总在双曲正弦函数图象 $C_2$ 上方
$\text{D.}$ 双曲正弦函数 $\sinh x=\frac{e^x-e^{-x}}{2}$ 导函数的图象与双曲余弦函数图象重合
如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 的底面是边长为 3 的正方形, 侧棱长为 $4, E, F$ 分别在 $A B, B C$ 上, 且 $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A B} ,\overrightarrow{C F}=\frac{1}{3} \overrightarrow{C B}$, 过 $D_1, E, F$ 的平面记为 $a$, 则下 列说法中正确的个数是
① $D_1 F$ 与面 $A B C D$ 所成角的正切值为 $\frac{2 \sqrt{10}}{5}$;
②平面 $a$ 截直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的 形状为四边形;
③平面 $a$ 将直四棱柱分割成的上、下两部分的体积之比 为 $3: 1$;
④)平面 $a$ 截直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的 面积为 $7 \sqrt{3}$;
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知集合 $A=\left\{x \mid x^2-4 x-5 < 0\right\}, B=\left\{y \mid y=\ln \left(x^2+1\right)\right\}$, 则 $A \cap B=$
$\text{A.}$ $(-1,5)$
$\text{B.}$ $[0,5)$
$\text{C.}$ $(-1,+\infty)$
$\text{D.}$ $[0,1)$
已知平面向量 $a, b$ 满足 $|a|=2, b=(1,1),|a+b|=\sqrt{10}$, 则 $a$ 在 $b$ 上的投影向量的坐标为
$\text{A.}$ $\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
$\text{B.}$ $(1,1)$
$\text{C.}$ $(-1,-1)$
$\text{D.}$ $\left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
在 $\triangle A B C$ 中, “ $\tan A \tan B < 1$ ”是“ $\triangle A B C$ 为针角三角形”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2$, 过 $F_1$ 作直线 $l$ 与 $C$ 的左、右两支分 别交于 $M, N$ 两点, 且 $\triangle M N F_2$ 是以 $\angle M N F_2$ 为顶角的等腰直角三角形, 若 $C$ 的离心率为 $e$, 则 $e^2=$
$\text{A.}$ $5+3 \sqrt{3}$
$\text{B.}$ $5+3 \sqrt{2}$
$\text{C.}$ $5+2 \sqrt{2}$
$\text{D.}$ $5+2 \sqrt{3}$
若不等式 $\mathrm{e}^{x-1}-m x-2 n-3 \geqslant 0$ 对 $\forall x \in \mathbf{R}$ 恒成立, 其中 $m \neq 0$, 则 $\frac{n}{m}$ 的最大值为
$\text{A.}$ $-\frac{\ln 3 \mathrm{e}}{2}$
$\text{B.}$ $-\ln 3 \mathrm{e}$
$\text{C.}$ $\ln 3 e$
$\text{D.}$ $\frac{\ln 3 e}{2}$
已知集合 $M=\left\{y \mid y=2^x\right\}, N=\left\{y \mid y=\sqrt{1-x^2}\right\}$, 则 $M \cap N=$
$\text{A.}$ $\{x \mid 0 < x < 1\}$
$\text{B.}$ $\{x \mid 0 < x \leqslant 1\}$
$\text{C.}$ $\{x \mid x \leqslant 1\}$
$\text{D.}$ $\{x \mid x>0\}$
已知向量 $a=(-2, m), b=(1,-2)$, 若 $a \perp b$, 则 $m$ 的值为
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ 2
$\text{D.}$ -2
“ $m=-1$ "是“直线 $l_1: m x+2 y+1=0$ 与直线 $l_2: \frac{1}{2} x+m y+\frac{1}{2}=0$ 平行" 的
$\text{A.}$ 充要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充分不必要条件
$\text{D.}$ 即不充分也不必要条件
若曲线 $y=\ln x+x^2$ 的一条切线的斜率为 3 , 则该切线的方程可能为
$\text{A.}$ $3 x-y-1=0$
$\text{B.}$ $3 x-y+1=0$
$\text{C.}$ $3 x-y-2=0$
$\text{D.}$ $3 x-y-1-\ln 2=0$
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $A B=2, P$ 为 $C C_1$ 的中点, 点 $Q$ 在四边形 $D C C_1 D_1$ 内 (包括边界)运动, 若 $A Q / /$ 平面 $A_1 B P$, 则 $A Q$ 的最小值为
$\text{A.}$ $1$
$\text{B.}$ $\frac{3 \sqrt{2}}{2}$
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $\sqrt{7}$
已知点 $M$ 在抛物线 $C: y^2=2 p x(p>0)$ 上, 若以点 $M$ 为圆心半径为 5 的圆与抛物线 $C$ 的准 线相切, 且与 $x$ 轴相交的弦长为 6 , 则 $p=$
$\text{A.}$ 2
$\text{B.}$ 8
$\text{C.}$ 2 或 8
$\text{D.}$ 6
已知集合 $A=\left\{x \mid x^2-2 x-3 < 0\right\}, B=\{x \mid y=\lg (x-1)\}$, 则 $A \cap B=$
$\text{A.}$ $(3,+\infty)$
$\text{B.}$ $(-1,+\infty)$
$\text{C.}$ $(-1,1)$
$\text{D.}$ $(1,3)$
已知边长为 2 的等边 $\triangle A B C, O$ 为其中心, 对(1) $|\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}|=6$; (2) $\overrightarrow{A B} \cdot \overrightarrow{A C}=2$;
(3) $|\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}|=0$; (4) $3 \overrightarrow{A O} \cdot \overrightarrow{O B}=2$ 这四个等式, 正确的个数是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
有一个圆台型的密闭盒子 (表面不计厚薄), 其母线与下底面成 $60^{\circ}$ 角, 且母线长恰好等于上下底 半径之和, 在圆台内放置一个球, 当球体积最大时, 设球的表面积为 $S_1$, 圆台的侧面积为 $S_2$, 则 ( )
$\text{A.}$ $S_1>S_2$
$\text{B.}$ $S_1 < S_2$
$\text{C.}$ $S_1=S_2$
$\text{D.}$ 无法确定 $S_1$ 与 $S_2$ 的大小
在 $\triangle A B C$ 中, $A B=5, A C=3, \tan A=\frac{4}{3}$, 点 $M, N$ 分别在边 $A B, B C$ 移动, 且 $M N=B N$, 沿 $M N$ 将 $\triangle B M N$ 折起来得到棱雉 $B-A M N C$, 则该棱雉的体积的最大值是
$\text{A.}$ $\frac{16 \sqrt{2}}{15}$
$\text{B.}$ $\frac{16 \sqrt{3}}{15}$
$\text{C.}$ $\frac{16 \sqrt{6}}{15}$
$\text{D.}$ $\frac{309}{128}$
如图, 正四棱台 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $E, F, G$ 分别是 棱 $C_1 D_1, D_1 A_1, A_1 B_1$ 的中点, 则下列判断中, 不正确的是
$\text{A.}$ $B, B_1, D_1, D$ 共面
$\text{B.}$ $F \in$ 平面 $A C E$
$\text{C.}$ $F G \perp$ 平面 $A C E$
$\text{D.}$ $A_1 C_1 / /$ 平面 $A C E$
若 $2 x-1=\sqrt{(x-2)^2+y^2}$, 则 $\sqrt{(x+2)^2+y^2}+\sqrt{(x-2)^2+y^2}$ 的最小值是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4