一、单选题 (共 40 题 ),每题只有一个选项正确
1. 已知 是偶函数, 则
-2
-1
1
2
2. 设 为平面坐标系的坐标原点, 在区域 内随机取一点, 记该点为 , 则直线 的 倾斜角不大于 的概率为
3. 甲乙两位同学从 6 种课外读物中各自选读 2 种, 则这两人选读的课外读物中恰有 1 种相同的选法共有
30 种
60 种
120 种
240 种
4. 如图, 是某校随机抽取 50 名学生的身高与体重的 散点图, 则下列说法正确的是
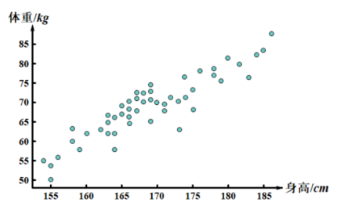
身高越高, 体重越重;
身高越高, 体重越轻;
身高与体重成正相关;
身高与体重成负相关.
5. 设 , 函数 在 上的最小值为 , 在 上的最小值为 , 当 变化时, 则下列选 项不可能的是
6. , 都有 , 则
存在 , 使得
存在 . 使得
7. 要得到函数 的图象, 只需将指数函数 的图象
向左平移 1 个单位
向右平移 1 个单位
向左平移 个单位
向右平移 个单位
8. 将函数 的图象上的点横坐标变为原来的 (纵坐标变) 得到函数 的图象, 若 存在 , 使得 对任意 恒成立, 则 .
9. 已知 的展开式中所有项的系数和为 512 , 则展开式中的常数项为
-756
756
-2268
2268
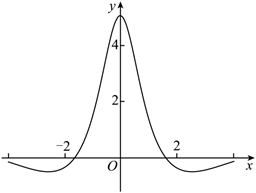
10. 函数
的图象如下图所示, 则
的解析式可能为
11. 已知函数 的一条对称轴为直线 , 一个周期为 4 , 则 的解析式可能为
12. 调查某种群花萼长度和花瓣长度,所得数据如图所示,其中相关系数r=0.8245,下列说法正确的是
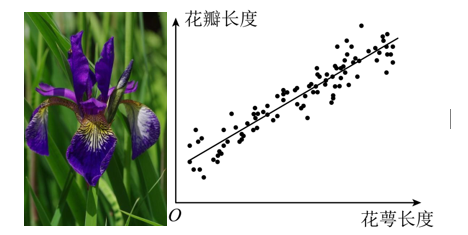
花瓣长度和花萼长度没有相关性
花瓣长度和花萼长度呈现负相关
花瓣长度和花萼长度呈现正相关
若从样本中抽取一部分,则这部分的相关系数一定是0.8245
13. 雅礼女篮一直是雅礼中学的一张靓丽的名片, 在刚刚结束的 2022 到 2023 赛季中国高中篮球联赛女子组 总决赛中, 雅礼中学女篮队员们敢打敢拼, 最终获得了冠军. 在颁奖仪式上, 女篮队员 12 人 (其中 1 人为 队长), 教练组 3 人, 站成一排照相, 要求队长必须站中间, 教练组-人要求相邻并站在边上, 总共有多少种站法
14. 函数 的图象大致为
15. 三名同学到五个社区参加社会实践活动, 要求每个社区有且只有一名同学, 每名同学至多去 两个社区,则不同的派法共有
90 种
180 种
125 种
243 种
16. 为了庆祝中国共产党第二十次全国代表大会, 学校采用按比例分配的分 层随机抽样的方法从高一 1002 人, 高二 1002 人, 高三 1503 人中抽取 126 人观看 “中国共产党第二十次全国代表大会”直播, 那么高三年级被 抽取的人数为
36
42
50
54
17. 某学生进行投篮训练, 采取积分制, 有 7 次投篮机会, 投中一次得 1 分, 不 中得 0 分, 若连续投中两次则额外加 1 分, 连续投中三次额外加 2 分, 以此 类推, 连续投中七次额外加 6 分, 假设该学生每次投中的概率是 , 且每次 投中之间相互独立, 则该学生在此次训练中恰好得 7 分的概率是
18. 设 , 则
19. 下列函数为奇函数且在 上为减函数的是
20. 已知 , 则 的值为
1
0
21. 已知 , 则 的大小关系是
22. 下列区间中, 函数 单调递增的区间是
23. 若 , 且 , 则
24. 甲、乙, 丙、丁等六名退休老党员相约去观看党史舞台剧 《星火》. 《星火》的票价为 50 元 / 人, 每人 限购一张票. 甲、乙、丙三人各带了一张 50 元钞, 其余三人各带了一张 100 元钞. 他们六人排成一列到 售票处买票, 而售票处一开始没有准备 50 元零钱, 那么他们六人共有多少种不同排队顺序能使购票时售 票处不出现找不出钱的状态.
720
360
180
90
25. 从 、、、、、、 这 7 个数中任取 5 个不同的数, 事件 “取出的 5 个不同的数的中位数是 4 ”, 事件 : “取出的 5 个不同的数的平均数是 4 ”, 则
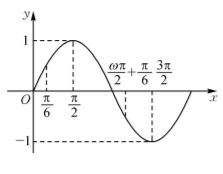
26. 已知函数
在区间
内有最大值, 但无最小值, 则
的取值范 围是
27. 设 , 则
28. 在党中央的正确领导下, 我国坚定不移贯彻新发展理念, 着力推进高质量发展, 推动构建新发展格局, 实施供给侧结构性改革, 制定一系列具有全局性意义的区域重大战略, 经济实力实现历史性跃升. 国内生产总值 (GDP) 从五十四万亿元增长到一百一十四万亿元, 稳居世界第二位.下表是 2022 年我国大陆 31 省市区 GDP 数据.
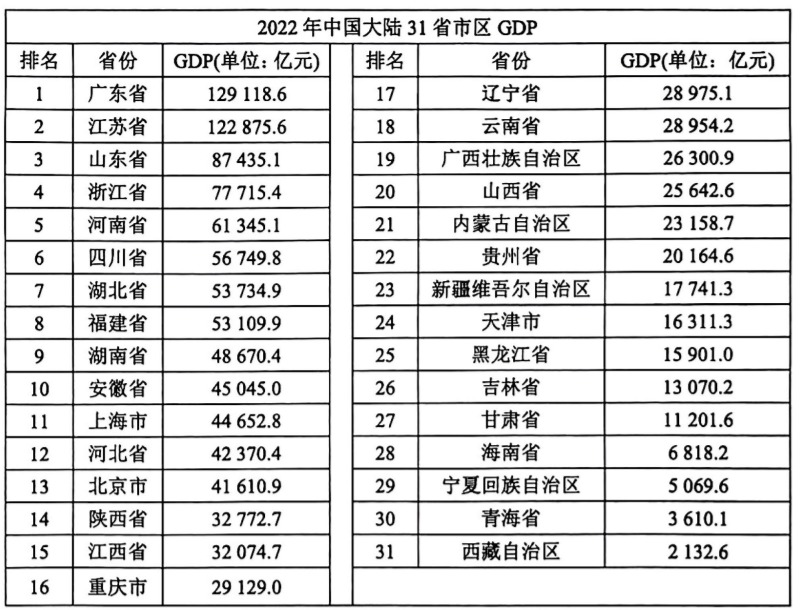
则由各省市区 GDP 组成的这组数据的第 75 百分位数为 (单位: 亿元)
16311.3
17741.3
48670.4
53109.9
29. 某地区有 20000 名考生参加了高三第二次调研考试. 经过数据分析, 数学成绩 近似服从正态分布 , 则数学成绩位于 的人数约为
参考数据: , .
455
2718
6346
9545
30. 有一组样本数据 , 则
这组样本数据的极差不小于 4
这组样本数据的平均数不小于 4
这组样本数据的中位数不小于 3
这组样本数据的众数等于 3
31. 设集合 和 都是自然数集合 ,映射 把集合 中的元素 映射到集合 中的元素 , 则在映射 下, 象 20 的原象是
2
3
4
5
32. 已知 , 那么下列命题成立的是
若 、 是第一象限角, 则
若 、 是第二象限角, 则
若 、 是第三象限角, 则
若 、 是第四象限角, 则
34. 若 , 则
35. 已知 , 则
36. 设 则
37. 已知函数 ,若 ,则
38. 设 , 则
39. 已知正数 满足 , 下列说法正确的是
40. 已知 . 设 , 则