一、单选题 (共 45 题,每小题 5 分,共 50 分,每题只有一个选项正确)
若 $\left(a x^2+\frac{3}{x}\right)^{10}$ 的展开式中系数最大的项有两项, 则正整数 $a$ 的所有可能取值之和为
$\text{A.}$ 30
$\text{B.}$ 33
$\text{C.}$ 58
$\text{D.}$ 51
已知随机变量 $\xi_i$ 满足 $P\left(\xi_i=1\right)=p_i, P\left(\xi_i=0\right)=1-p_i, i=1$, 2. 若 $\frac{1}{2} < p_1 < p_2 < 1$, 则
$\text{A.}$ $E\left(\xi_1\right)>E\left(\xi_2\right), D\left(\xi_1\right) < D\left(\xi_2\right)$
$\text{B.}$ $E\left(\xi_1\right)>E\left(\xi_2\right), D\left(\xi_1\right)>D\left(\xi_2\right)$
$\text{C.}$ $E\left(\xi_1\right) < E\left(\xi_2\right), D\left(\xi_1\right) < D\left(\xi_2\right)$
$\text{D.}$ $E\left(\xi_1\right) < E\left(\xi_2\right), D\left(\xi_1\right)>D\left(\xi_2\right)$
某地投资 $a$ 亿元进行基础建设, $t$ 年后产生的社会经济效益为 $f(t)=a e^{\lambda t}$ 亿元, 若该地投资基础建设 4 年后产生的社会经济效益是投资额的 2 倍, 且再过 $t_1$ 年, 该项投资产生的社会经济效益是投资额的 8 倍, 则 $t_1=$
$\text{A.}$ 4
$\text{B.}$ 8
$\text{C.}$ 12
$\text{D.}$ 16
从集合 $S=\{x \in N \mid 1 \leq x \leq 10\}$ 中任取 3 个不同的数, 它们的和能被 3 整除的概率为
$\text{A.}$ $\frac{3}{10}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{41}{120}$
$\text{D.}$ $\frac{7}{20}$
将一枚均匀的骰子独立投掷两次,所得的点数依次记为 $x, y$, 记 $A$ 事件为 “ $\mathrm{C}_8^x
> \mathrm{C}_8^y$ ”, 则 $P(A)=$
$\text{A.}$ $\frac{11}{36}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{13}{36}$
$\text{D.}$ $\frac{5}{12}$
秋冬季节是某呼吸道疾病的高发期, 为了解该疾病的发病情况, 疾控部门对该地区居民进行普查化验, 化验结果阳性率为 $1.97 \%$,但统计分析结果显示患病率为 $1 \%$. 医学研究表明化验结果是有可能存在误差的,没有患该疾病的居民其化验结果呈阳性的概率为 0.01 ,则该地区患有该疾病的居民化验结果呈阳性的概率为
$\text{A.}$ 0.96
$\text{B.}$ 0.97
$\text{C.}$ 0.98
$\text{D.}$ 0.99
已知变量 $x, y$ 之间的线性回归方程为 $\hat{y}=2 x+1$, 且变量 $x, y$ 之间的一组相关数据如表所示,

则下列说法正确的是
$\text{A.}$ $m=17$
$\text{B.}$ 变量 $y$ 与 $x$ 是负相关关系
$\text{C.}$ 该回归直线必过点 $(5,11)$
$\text{D.}$ $x$ 增加 1 个单位, $y$ 一定增加 2 个单位
“二十四节气”是中国古代劳动人民伟大的智慧结晶,其划分如图所示,小明打算在网上搜集一些与二十四节气有关的古诗,他准备在春季的6个节气与夏季的6个节气中共选出3个节气,若春季的节气和夏季的节气各至少选出1个,则小明选取节气的不同情况的种数是

$\text{A.}$ $90$
$\text{B.}$ $180$
$\text{C.}$ $270$
$\text{D.}$ $360$
一个袋子中有大小和质地相同的4个球,其中有2个红球,2个黄球,每次从中随机摸出1个球,摸出的球不再放回,则第二次摸到黄球的条件下,第一次摸到红球的概率为
$\text{A.}$ $\dfrac{1}{3}$
$\text{B.}$ $\dfrac{1}{2}$
$\text{C.}$ $\dfrac{2}{3}$
$\text{D.}$ $\dfrac{3}{4}$
样本数据 $16,24,14,10,20,30,12,14,40$ 的中位数为
$\text{A.}$ 14
$\text{B.}$ 16
$\text{C.}$ 18
$\text{D.}$ 20
甲、乙、丙等 5 人站成一排, 且甲不在两端, 乙和丙之间恰有 2 人, 则不同排法共有
$\text{A.}$ 20 种
$\text{B.}$ 16 种
$\text{C.}$ 12 种
$\text{D.}$ 8 种
将 1 到 50 这 50 个正整数平分成甲乙两组, 每组各 25 个数, 使得甲组的中位数比乙组的中位数小 1 - 试问共有几种分法?
$\text{A.}$ $C_{25}^{50}$
$\text{B.}$ $C_{24}^{48}$
$\text{C.}$ $C_{12}^{24}$
$\text{D.}$ $\left(C_{12}^{24}\right)^2$
某实验室收集了大量的 $A 、 B$ 两相似物种, 记录其身长为 $x$ (单位:公分) 与体重 $y$ (单位:公克), 得 $A 、 B$ 两物种的平均身长分别为 $\overline{x_A}=5.2 、 \overline{x_B}=6$, 标准差分别为 $0.3 、 0.1 $。
令 $A 、 B$ 两物种的平均体重分别为 $\overline{y_A} 、 \overline{y_B}$ 。若 $A 、 B$ 两物种其体重 $y$ 对身长 $x$ 的回归直线分别为 $L_A: y=2 x-0.6 、 L_B: y=1.5 x+0.4$, 相关系数分别为 $0.6 、 0.3$ 。今发现一只身长 5.6 公分、体重 8.6 公克的个体 $P$, 试选出正确的选项。
$\text{A.}$ $\overline{y_A} < \overline{y_B}$
$\text{B.}$ $A$ 物种的体重标准差小于 $B$ 物种的体重标准差
$\text{C.}$ 就 $A$ 物种而言, 个体 $P$ 的体重与平均体重 $\overline{y_A}$ 之差的绝对值大于一个标准差
$\text{D.}$ 点 $(5.6,8.6)$ 到直线 $L_A$ 的距离小于其到直线 $L_B$ 的距离
考虑二元一次方程组 $\left\{\begin{array}{l}a x+6 y=6 \\ x+b y=1\end{array}\right.$, 其系数 $a, b$ 之值分别由投掷一颗公正骰子与一枚均匀硬币来决定。令 $a$ 值为骰子出现之点数; 若硬币出现正面时 $b$ 值为 1 , 若硬币出现反面时 $b$ 值为 2 。试选出正确的选项。
$\text{A.}$ 掷出 $a=b$ 的机率为 $\frac{1}{3}$
$\text{B.}$ 此方程组无解的机率为 $\frac{1}{12}$
$\text{C.}$ 此方程组有唯一解的机率为 $\frac{5}{6}$
$\text{D.}$ 硬币出现反面且此方程组有解的机率为 $\frac{1}{2}$
已知 $m, n$ 都是正整数, 且 $m < n$, 下列有关组合数的计算, 正确的是
$\text{A.}$ $C_n^m=C_n^{n-m}$
$\text{B.}$ $C_{n-1}^m+C_{n-1}^{m-1}=C_n^{m+1}$
$\text{C.}$ $m C_n^m=n C_{n-1}^{m-1}$
$\text{D.}$ $\left(C_n^0\right)^2+\left(C_n^1\right)^2+\cdots+\left(C_n^n\right)^2=C_{2 n}^n$
数据 $68,70,80,88,89,90,96,98$ 的第 15 百分位数为
$\text{A.}$ 69
$\text{B.}$ 70
$\text{C.}$ 75
$\text{D.}$ 96
为了更好的了解党的历史, 宣传党的知识, 传颂英雄事迹, 某校团支部 6 人组建了 “党史宣讲” 、“歌曲演唱” 、“诗歌创作” 三个小组, 每组 2 人, 其中甲不会唱歌, 乙不能胜任诗歌创作, 则组建方法有种
$\text{A.}$ 60
$\text{B.}$ 72
$\text{C.}$ 30
$\text{D.}$ 42
某校高一年级 18 个班参加艺术节合唱比赛, 通过简单随机抽样, 获得了 10 个班的比赛得分如下: $91,89,90,92,94,87,93,96,91,85$, 则这组数据的 $80 \%$ 分位数为
$\text{A.}$ 93
$\text{B.}$ 93.5
$\text{C.}$ 94
$\text{D.}$ 94.5
甲、乙、丙等 5 名同学参加政史地三科知识竞赛, 每人随机选择一科参加竞赛, 则甲和乙不参加同一科, 甲和丙参加同一科竞赛, 且这三科竞赛都有人参加的概率为
$\text{A.}$ $\frac{4}{81}$
$\text{B.}$ $\frac{2}{27}$
$\text{C.}$ $\frac{10}{81}$
$\text{D.}$ $\frac{4}{27}$
$A, B, C, D, E$ 五人站成一排, 如果 $A, B$ 必须相邻, 那么排法种数为
$\text{A.}$ 24
$\text{B.}$ 120
$\text{C.}$ 48
$\text{D.}$ 60
数据 $6.0,7.4,8.0,8.4,8.6,8.7,9.0,9.1$ 的 50 百分位数为
$\text{A.}$ 8.4
$\text{B.}$ 8.5
$\text{C.}$ 8.6
$\text{D.}$ 8.7
在某次美术专业测试中, 若甲、乙、丙三人获得优秀等级的概率分别是 $0.6,0.7$ 和 0.5 , 且三人的测试结果相互独立, 则测试结束后, 在甲、乙、丙三人中恰有两人没达优秀等级的前提条件下, 乙没有达优秀等级的概率为
$\text{A.}$ $\frac{15}{29}$
$\text{B.}$ $\frac{7}{8}$
$\text{C.}$ $\frac{5}{8}$
$\text{D.}$ $\frac{17}{29}$
某校高一年级 18 个班参加艺术节合唱比赛, 通过简单随机抽样, 获得了 10 个班的比赛得分如下: $91,89,90,92,94,87,93,96,91,85$, 则这组数据的 $80 \%$ 分位数为
$\text{A.}$ 93
$\text{B.}$ 93.5
$\text{C.}$ 94
$\text{D.}$ 94.5
古城赣州最早有五大城门, 分别为镇南门、百盛门、涌金门、建春门和西津门, 赣州某学校历史兴趣小组决定利用两个周日的时间对五大城门的地理位置及历史意义进行调研. 若约定: 每个城门只调研一次, 且每个周日只调研五大城门中的两大城门或三大城门, 则恰好在同一个周日调研百盛门和建春门的概率为
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{4}{5}$
在党的二十大报告中, 习近平总书记提出要发展 “高质量教育”, 促进城乡教育均衡发展. 某地区教育行政部门积极响应党中央号召, 近期将安排甲、乙、丙、丁 4 名教育专家前往某省教育相对落后的三个地区指导教育教学工作, 则每个地区至少安排 1 名专家的概率为
$\text{A.}$ $\frac{1}{9}$
$\text{B.}$ $\frac{4}{9}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{8}{27}$
现有甲、乙两组数据, 每组数据均由六个数组成, 其中甲组数据的平均数为 3 , 方差为 5 , 乙组数据的平均数为 5 , 方差为 3 . 若将这两组数据混合成一组, 则新的一组数据的方差为
$\text{A.}$ 3.5
$\text{B.}$ 4
$\text{C.}$ 4.5
$\text{D.}$ 5
有 5 辆车停放 6 个并排车位, 货车甲车体较宽, 停靠时需要占两个车位, 并且乙车不与货车甲相邻停放,则共有 ________ 种停放方法
$\text{A.}$ 72
$\text{B.}$ 144
$\text{C.}$ 108
$\text{D.}$ 96
如图为 2021 2022 年中国十大行业人工智能应用渗透率, 则下列说法错误的是
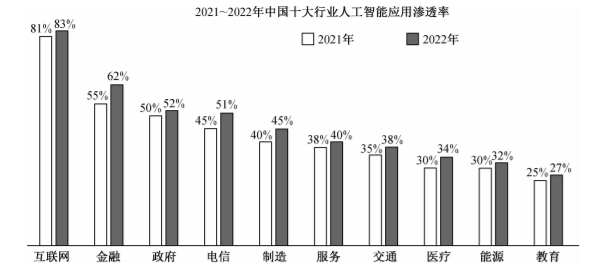
$\text{A.}$ 2021 年与 2022 年人工智能应用渗透率最低的行业都是教育
$\text{B.}$ 与 2021 年相比, 2022 年人工智能应用渗透率增长最快的是金融行业
$\text{C.}$ 2021 年十大行业人工智能应用渗透率的极差为 $56 \%$
$\text{D.}$ 2022 年十大行业人工智能应用渗透率的中位数是 $42.5 \%$
《易・系辞上》有 “河出图, 洛出书”之说, 河图、洛书是中华文化, 阴阳术数之源, 其中河图排列结构是一、六在后, 二、七在前, 三、八在左, 四、九在右, 五、十背中. 如图, 白点为阳数, 黑点为阴数.若从这 10 个数中任取 3 个数, 已知 3 个数中至多有 1 个阴数, 则取出的 3 个数之和是 5 的倍数的概率是
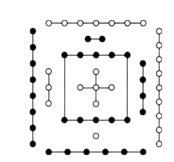
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
$\left(x^2-x+y\right)^5$ 的展开式中 $x^5 y^2$ 的系数为
$\text{A.}$ -30
$\text{B.}$ -20
$\text{C.}$ 20
$\text{D.}$ 30
某校高一年级 15 个班参加朗诵比赛的得分如下: 85 87 88 89 89 90 91 91 92 93 93 93 94 96 98 ,则这组数据的 $40 \%$ 分位数为
$\text{A.}$ 90
$\text{B.}$ 91
$\text{C.}$ 90.5
$\text{D.}$ 92
高一 (1) 班有 8 名身高都不相同的同学去参加红歌合唱, 他们站成前后对齐的 2 排, 每排 4 人, 则前排的同学都比后排对应的同学矮的概率为
$\text{A.}$ $\frac{1}{384}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{3}{8}$
$\text{D.}$ $\frac{1}{16}$
50 个队伍进行排球单循环赛, 胜一局积 1 分, 负一局积 0 分, 且任取 27 支队伍都能找到一个全部战胜其余 26 支队伍和一支全部负于其余 26 支队伍的, 问这 50 支队伍最少共有 ________ 种不同的积分
$\text{A.}$ 50
$\text{B.}$ 45
$\text{C.}$ 27
$\text{D.}$ 以上选项均不对
某旅行社为迎节日搞活动旅游, 经市场调查, 某旅游线路销量 $Y$ (人) 与旅游价格 $X$ (元/人) 负相关, 则其回归直线方程可能是
$\text{A.}$ $Y=-80 X+1600$
$\text{B.}$ $Y=80 X+1600$
$\text{C.}$ $Y=-80 X-1600$
$\text{D.}$ $Y=80 X-1600$
$A, B, C, D, E$ 五人站成一排, 如果 $A, B$ 必须相邻, 那么排法种数为
$\text{A.}$ 24
$\text{B.}$ 180
$\text{C.}$ 48
$\text{D.}$ 60
样本数据 $5,7,4,6,12,10,11,9$ 的第 70 百分位数为
$\text{A.}$ 7
$\text{B.}$ 9
$\text{C.}$ 9.5
$\text{D.}$ 10
甲、乙、丙、丁、戊 5 位同学报名参加学校举办的三项不同活动, 每人只能报其中一项活动, 每项活动至少有一个人参加, 则甲、乙、丙三位同学所报活动各不相同的概率为
$\text{A.}$ $\frac{5}{18}$
$\text{B.}$ $\frac{6}{25}$
$\text{C.}$ $\frac{9}{25}$
$\text{D.}$ $\frac{8}{9}$
有甲、乙等五人到三家企业去应聘, 若每人至多被一家企业录用, 每家企业至少录用其中一人且甲、乙两人不能被同一家企业录用,则不同的录用情况种数是
$\text{A.}$ 60
$\text{B.}$ 114
$\text{C.}$ 278
$\text{D.}$ 336
5 名同学到 3 个小区参加垃圾分类宣传活动, 每名同学只去 1 小区, 每个小区至少安排 1 名同学, 则不同的安排方法共有
$\text{A.}$ 60 种
$\text{B.}$ 90 种
$\text{C.}$ 150 种
$\text{D.}$ 240 种
某中学举行数学解题比赛, 其中 5 人的比赛成绩分别为 $70,85,90,75,95$, 则这 5 人成绩的上四分位数是
$\text{A.}$ 90
$\text{B.}$ 75
$\text{C.}$ 95
$\text{D.}$ 70