一、单选题 （共 43 题，每小题 5 分，共 50 分，每题只有一个选项正确）
如图, 四个等腰直角三角形拼成一个正方形, 则阴影部分的面积为
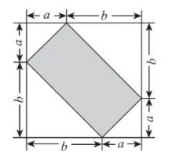
$\text{A.}$ $a^2+b^2$
$\text{B.}$ $a^2-b^2$
$\text{C.}$ $2 a b$
$\text{D.}$ $4 a b$
如图, 菱形 $A B C D$ 的对角线 $A C, B D$ 交于点 $O, A C=4, B D=16$, 将 $\triangle A B O$ 沿点 $A$ 到点 $C$ 的方向平移, 得 到 $\triangle A^{\prime} B^{\prime} O^{\prime}$. 当点 $A^{\prime}$ 与点 $C$ 重合时, 点 $A$ 与点 $B^{\prime}$ 之间的距离为
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ 12
在矩形 $A B C D$ 中, 点 $E$ 为 $A D$ 中点, 点 $F$ 为 $C D$ 中点, 连接 $B F 、 C E$ 交于点 $G$, 若 $A B=4, \angle D C E=2 \angle C B F$, 则线段 $B G$ 的长为
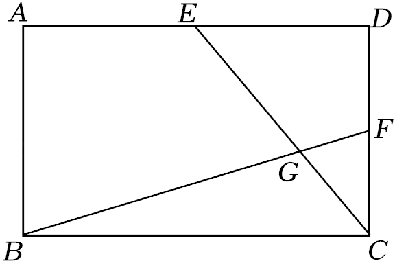
$\text{A.}$ $\frac{8 \sqrt{10}}{5}$
$\text{B.}$ $2 \sqrt{10}$
$\text{C.}$ $4$
$\text{D.}$ $\frac{3}{2} \sqrt{10}$
如图, 在正方形 $A B C D$ 中, $A E$ 平分 $\angle B A C$ 交 $B C$ 于点 $E$, 点 $F$ 是边 $A B$ 上一点, 连接 $D F$, 若 $B E=C E$, 则 $\angle C D F$ 的度数为
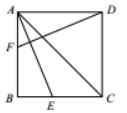
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $67.5^{\circ}$
$\text{D.}$ $77.5^{\circ}$
在菱形 $A B C D$ 中, 对角线 $A C$ 与 $B D$ 相交于点 $O$, 再添加一个条件, 仍不能判定四边形 $A B C D$ 是矩形的是
$\text{A.}$ $A B=A D$
$\text{B.}$ $O A=O B$
$\text{C.}$ $ AC=B D$
$\text{D.}$ $DC \perp B C$
如图, 在矩形 $A B C D$ 中, 对角线 $A C$ 与 $B D$ 相交于点 $O$, 已知 $\angle A C B=25^{\circ}$, 则 $\angle A O B$ 的大小是
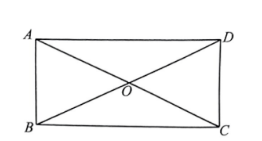
$\text{A.}$ $130^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $25^{\circ}$
如图, 已知正方形 $A B C D$ 的边长为 $4, E$ 是 $A B$ 边延长线上一点, $B E=2, F$ 是 $A B$ 边上 一点, 将 $\triangle C E F$ 沿 $C F$ 翻折, 使点 $E$ 的对应点 $G$ 落在 $A D$ 边上, 连接 $E G$ 交折痕 $C F$ 于点 $H$, 则 $F H$ 的长是
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{\sqrt{10}}{3}$
$\text{C.}$ $1$
$\text{D.}$ $\frac{\sqrt{5}}{3}$
如图, 已知四边形 $A B C D$ 为等腰梯形, $A D / / B C, A B=C D, A D=\sqrt{2}, E$ 为 $C D$ 中点, 连接 $A E$, 且 $A E=2 \sqrt{3}, \angle D A E=30^{\circ}$, 作 $A E \perp A F$ 交 $B C$ 于 $F$, 则 $B F=$
$\text{A.}$ $1$
$\text{B.}$ $3-\sqrt{3}$
$\text{C.}$ $\sqrt{5}-1$
$\text{D.}$ $4-2 \sqrt{2}$
如图, 已知 $I_1 / / I_2 / / I_3$, 相邻两条平行直线间的距离相等, 若等腰直角 $\triangle A B C$ 的三个顶 点分别在这三条平行直线上, 则 $\sin a$ 的值是
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{6}{17}$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{10}}{10}$
如图, $E$ 是正方形 $A B C D$ 内一点, $A E \perp D E$ 于 $E, A E=2 \mathrm{~cm}$, 则 $\triangle{A B E}$ 的面积是( ) $\mathrm{cm}^2$.
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 3
$\text{D.}$ 2
如图, 在平面直角坐标系中, 已知 $A(-3,-2), B(0,-2), C(-3,0), M$ 是线段 $A B$ 上的
一个动点, 连接 $C M$, 过点 $M$ 作 $M N \perp M C$ 交 $y$ 轴于点 $N$. 若点 $M, N$ 在直线 $y=k x+b$ 上, 则 $b$ 的最大值是
$\text{A.}$ $-\frac{7}{8}$
$\text{B.}$ $-\frac{3}{4}$
$\text{C.}$ $-1$
$\text{D.}$ $-\frac{7}{4}$
如图, 在菱形 $A B C D$ 中, 对角线 $A C 、 B D$ 交于点 $O$, 以 $A C$ 为斜边作 $R t \triangle A E C, A E$ 与 $B D$ 交于点 $F$, 连接 $B E$, 使得 $B F=C O$, 且 $\angle E B F=2 \angle C A E$, 若 $A C=2$, 则菱形 $A B C D$ 的周长为
$\text{A.}$ $4 \sqrt{6}$
$\text{B.}$ $4 \sqrt{3}$
$\text{C.}$ $4 \sqrt{2}$
$\text{D.}$ $4$
如图, 棱形 $A B C D$ 中, 对角线 $A C 、 B D$ 相交于点 $O, H$ 为 $A D$ 边中点, 棱形 $A B C D$ 的周长为 $20, B D=8$. 则 $\tan \angle H O D$ 的值等于
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{4}{3}$
如图, 在正方形 $A B C D$ 中, 点 $E 、 F$ 分别在边 $A D$ 和 $C D$ 上, $ A F \perp B E$, 垂足为 $G$, 若 $\frac{A E}{E D}=2$, 则 $\frac{A G}{G F}$ 的值为
$\text{A.}$ $\frac{4}{5}$
$\text{B.}$ $\frac{5}{6}$
$\text{C.}$ $\frac{6}{7}$
$\text{D.}$ $\frac{7}{8}$
如图, 若方格纸中每个小正方形的边长均为 1 , 则阴影部分的面积为
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ $\frac{16}{3}$
$\text{D.}$ $\frac{17}{3}$
如图, 在平行四边形 $A B C D$ 中, 点 $E 、 F 、 G$ 分别是 $A D 、 B C 、 C D$ 的中点, $B E \perp E G, A D=2 \sqrt{5}, A B=3$, 则 $A F$ 的长是
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
公元三世纪，我国汉代数学家赵爽在注解 《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等 的直角三角形与中间的小正方形拼成的一个大正方形. 如果大正方形的面积是 125 ，小正方形面积是 25 ，则 $(\sin \theta+\cos \theta)^2= $
$\text{A.}$ $\frac{9}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{5}$
$\text{C.}$ $\frac{3 \sqrt{5}}{5}$
$\text{D.}$ $\frac{1}{5}$
如图，将边长分别为10cm和4cm的矩形纸片沿着虚线剪成两个全等的梯形纸片．裁剪线与矩形较长边所夹的锐角是45°，则梯形纸片中较短的底边长为
$\text{A.}$ 2cm
$\text{B.}$ 2.5cm
$\text{C.}$ 3cm
$\text{D.}$ 3.5cm
如图, 在正方形 $A B C D$ 中, 点 $E, F$ 分别在 $B C, C D$ 上, 连接 $A E, A F, E F, \angle E A F=45^{\circ}$. 若 $\angle B A E=\alpha$, 则 $\angle F E C$ 一定等于
$\text{A.}$ $2 \alpha$
$\text{B.}$ $90^{\circ}-2 \alpha$
$\text{C.}$ $45^{\circ}-\alpha$
$\text{D.}$ $90^{\circ}-\alpha$
我国魏晋时期数学家刘徽在《九章算术注》中捉到了著名的“割圆术”, 即利用 圆的内接正多边形逼近圆的方法来近似估算, 指出“割之弥细, 所失弥少. 㓶之 又割, 以至于不可割, 则与圆周合体, 而无所失矣”. “割圆术” 军育了微积分思 想, 他用这种思想得到了圆周率 $\pi$ 的近似值为 3.1416 . 如图, $\odot O$ 的半径为 1 , 运用“割圆术”, 以圆内接正六边形面积近似估计 $\odot O$ 的面 积, 可得 $\pi$ 的估计值为 $\frac{3 \sqrt{3}}{2}$, 若用圆内接正十二边形作近似 估计, 可得 $\pi$ 的估计值为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 3
$\text{D.}$ $2 \sqrt{3}$
在四边形 $A B C D$ 中, $A D / / B C, A B=C D$, 下列说法能使四边形 $A B C D$ 为矩形的是
$\text{A.}$ $A B / / C D$
$\text{B.}$ $A D=B C$
$\text{C.}$ $\angle A=\angle B$
$\text{D.}$ $\angle A=\angle D$
已知在梯形 $A B C D$ 中, 联结 $A C 、 B D$, 且 $A C \perp B D$, 设 $A B=a, C D=b$, 下列两个结论:
(1) $A C=\frac{\sqrt{2}}{2}(a+b)$;
(2) $A D=\frac{\sqrt{2}}{2} \sqrt{a^2+b^2}$.
$\text{A.}$ (1)正确(2)错误
$\text{B.}$ (1)错误(2)正确
$\text{C.}$ (1)(2)均正确
$\text{D.}$ (1)(2)均不正确
如图, 边长为 6 的正方形 $A B C D$ 中, $M$ 为对角线 $B D$ 上的一点, 连接 $A M$ 并延 长交 $C D$ 于点 $P$, 若 $P M=P C$, 则 $A M$ 的长为
$\text{A.}$ $3(\sqrt{3}-1)$
$\text{B.}$ $3(3 \sqrt{3}-2)$
$\text{C.}$ $6(\sqrt{3}-1)$
$\text{D.}$ $6(3 \sqrt{3}-2)$
通过下图面积的计算，验证一个恒等式，此等式是
$\text{A.}$ ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$
$\text{B.}$ ${{\left( a-b \right)}^{2}}+4ab={{\left( a+b \right)}^{2}}$
$\text{C.}$ ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$
$\text{D.}$ ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$
如图, 若菱形 $A B C D$ 的周长 $16 \mathrm{~cm}$, 则菱形 $A B C D$ 的一边的中点 $E$ 到对角线交点 $O$ 的 距离为
$\text{A.}$ 1cm
$\text{B.}$ 2cm
$\text{C.}$ 3cm
$\text{D.}$ 4cm
已知四边形 $A B C D$ 是平行四边形, 下列结论中不正确的是
$\text{A.}$ 当 $A B=B C$ 时, 四边形 $A B C D$ 是菱形
$\text{B.}$ 当 $A C \perp B D$ 时, 四边形 $A B C D$ 是菱形
$\text{C.}$ 当 $\angle A B C=90^{\circ}$ 时, 四边形 $A B C D$ 是矩形
$\text{D.}$ 当 $A C=B D$ 时, 四边形 $A B C D$ 是正方形
如图, 正方形 $A B C D$ 的边长为 $8, M$ 在 $C D$ 上, 且 $D M=2, N$ 是 $A C$ 上的一个动点, 则 $D N+M N$ 的最小值为
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ $8 \sqrt{2}$
如图, 正五边形 $A B C D E$ 内接于 $\odot O$, 连接 $O C, O D$, 则 $\angle B A E-\angle C O D=$
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $54^{\circ}$
$\text{C.}$ $48^{\circ}$
$\text{D.}$ $36^{\circ}$
如图, 点 $E$ 在正方形 $A B C D$ 的对角线 $A C$ 上, $E F \perp A B$ 于点 $F$, 连接 $D E$ 并延长, 交边 $B C$ 于点 $M$, 交边 $A B$ 的延长线于点 $G$. 若 $A F=2, F B=1$, 则 $M G=(\quad)$
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $\frac{3 \sqrt{5}}{2}$
$\text{C.}$ $\sqrt{5}+1$
$\text{D.}$ $\sqrt{10}$
如图, 平行四边形 $A B C D$ 中, $P$ 是四边形内任意一点, $\triangle A B P, \triangle B C P, \triangle C D P, \triangle A D P$的面积分别为 $S_1, S_2, S_3, S_4$, 则一定成立的是
$\text{A.}$ $S_1+S_2=S_3+S_4$
$\text{B.}$ $S_1+S_2>S_3+S_4$
$\text{C.}$ $S_1+S_3=S_2+S_4$
$\text{D.}$ $S_1+S_2 < S_3+S_4$
学习《设计制作长方体形状的包装纸盒》后, 小宁从长方形硬纸片上截去两个矩形 (图中阴影部分), 再沿虚线折成一个无盖的长方体纸盒.纸片长为 $30 \mathrm{~cm}$, 宽为 $18 \mathrm{~cm}, A D=2 A B$, 则该纸盒的容积为
$\text{A.}$ $960 \mathrm{~cm}^3$
$\text{B.}$ $650 \mathrm{~cm}^3$
$\text{C.}$ $800 \mathrm{~cm}^3$
$\text{D.}$ $648 \mathrm{~cm}^3$
如图所示, $\square A B C D$ 中, 对角线 $A C, B D$ 交于点 $O, E$ 是 $C D$ 中点, 连接 $O E$, 若 $O E=3 \mathrm{~cm}$, 则 $A D$ 的长为
$\text{A.}$ $3 \mathrm{~cm}$
$\text{B.}$ $6 \mathrm{~cm}$
$\text{C.}$ $9 \mathrm{~cm}$
$\text{D.}$ $12 \mathrm{~cm}$
“赵爽弦图”巧妙地利用面积关系证明了勾股定理, 是我国古代数学的骄傲. 如图所示的“赵爽弦图” 是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设直角三角形较长直角边长为 $a$, 较短直角边长为 $b$. 若 $a b=6$, 大正方形的面积为 16 , 则小正方形的面积为
$\text{A.}$ 8
$\text{B.}$ 6
$\text{C.}$ 4
$\text{D.}$ 3
如图, 在平行四边形 $A B C D$ 和平行四边形 $B E F G$ 中, $A B=A D, B G=B E$, 点 $A 、 B 、 E$ 在同一直线上, $P$ 是线段 $D F$ 的中点, 连接 $P G, P C$. 若 $\angle A B C=\angle B E F=60^{\circ}$, 则 $\frac{P G}{P C}=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
长方形的周长为 $\mathrm{x}$, 宽为 2 , 则这个长方形的面积为
$\text{A.}$ $2 x$
$\text{B.}$ $2(x-2)$
$\text{C.}$ $x-4$
$\text{D.}$ $2 \cdot(x-2) / 2$
一个四边形, 对于下列条件: (1)一组对边平行, 一组对角相等; (2)一组对边平行, 一条对角线被另一条对角线平分; (3)一组对边相等, 一条对角线被另一条对角线平分; (4)两组对角的平分线分别平行, 不能判定为平行四边形的是
$\text{A.}$ (1)
$\text{B.}$ (2)
$\text{C.}$ (3)
$\text{D.}$ (4)
如图, 已知 $\mathrm{E}$ 是菱形 $\mathrm{ABCD}$ 的边 $\mathrm{BC}$ 上一点, 且 $\angle \mathrm{DAE}=\angle \mathrm{B}=80^{\circ}$, 那么 $\angle \mathrm{CDE}$ 的度数为
$\text{A.}$ $20^{\circ}$
$\text{B.}$ $25^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $35^{\circ}$
如图, 在梯形 $A B C D$ 中, $\angle A B C=90^{\circ}, A E / / C D$ 交 $B C$ 于 $E, 0$ 是 $A C$ 的中点, $A B=\sqrt{3}, A D=2$, $\mathrm{BC}=3$, 下列结论: (1) $\angle \mathrm{CAE}=30^{\circ}$; (2) $\mathrm{AC}=2 \mathrm{AB}$; (3) $\mathrm{S}_{\triangle \mathrm{ADC}}=2 \mathrm{~S}_{\triangle \mathrm{ABB}}$; (4) $\mathrm{BO} \perp \mathrm{CD}$, 其中正确的是
$\text{A.}$ (1)(2)(3)
$\text{B.}$ (2)(3)(4)
$\text{C.}$ (1)(3)(4)
$\text{D.}$ (1)(2)(3)(4)
已知点 $E, F$ 分别在正方形 $A B C D$ 的边 $C D, A D$ 上, $C D=4 C E, \angle E F B=\angle F B C$, 则 $\tan \angle A B F=$
$\text{A.}$ $\frac{1}{2}$.
$\text{B.}$ $\frac{3}{5}$.
$\text{C.}$ $\frac{\sqrt{2}}{2}$.
$\text{D.}$ $\frac{\sqrt{3}}{2}$.