单选题 (共 6 题 ),每题只有一个选项正确
在空间中存在与 $x O y$ 平面平行的匀强电场, $x 、 y$ 轴上电势随位置变化的图象如图所示, 则下列说 法正确的是
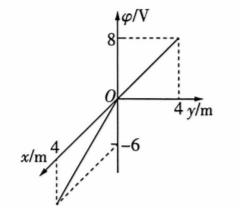
$\text{A.}$ 匀强电场的电场强度大小为 $2.5 \mathrm{~V} / \mathrm{m}$
$\text{B.}$ 坐标为 $(4 \mathrm{~m}, 3 \mathrm{~m})$ 的点的电势为 $-6 \mathrm{~V}$
$\text{C.}$ 正试探电荷位于第三象限时, 电势能大于零
$\text{D.}$ 电势为零的点连成的线对应的函数为 $y=\frac{4}{3} x$
如图甲所示, $P Q$ 为水平固定的绝缘细杆, 用等长的绝缘细线在 $P Q$ 上悬挂完全相同的两根导线 $a b 、 c d$, 图乙为沿 $P$ 到 $Q$ 方向观察时的截面图。当两导线中通人方向相反的电流 $I$ 时, 测得两悬线间的夹角 $\theta$ 为 $60^{\circ}$; 同时改变导线中通人的电流大小, 稳定时测得两悬线间的夹角 $\theta^{\prime}$ 为 $74^{\circ}$ 。 已知通电导线在周围某点产生的磁感应强度大小与该点到导线的距离成反比, 与导线中的电流 大小成正比。 $\sin 37^{\circ}=0.6$, 则第二次导线中的电流约为
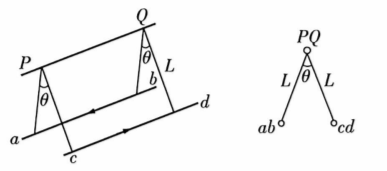
$\text{A.}$ $1.25 I$
$\text{B.}$ $1.56 I$
$\text{C.}$ $1.71 I$
$\text{D.}$ $1.85 I$
小明和小王在操场上练习投球和击球, 小明投球位置到地面的高度满足 $1.3 \mathrm{~m} \leqslant h_1 \leqslant 1.9 \mathrm{~m}$, 且 球始终沿水平方向投出; 小王击球位置到地面的高度满足 $0.1 \mathrm{~m} \leqslant h_2 \leqslant 0.5 \mathrm{~m}$, 且击球位置和投 球位置间的水平距离始终等于两同学间的距离, 为 $12 \mathrm{~m}$ 。重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$, 不考虑空气 阻力,下列说法正确的是
$\text{A.}$ 小明投球时球的最小初速度为 $15 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ 小明投球时球的最大初速度为 $30 \mathrm{~m} / \mathrm{s}$
$\text{C.}$ 小王击球时球的最大速度为 $31 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 小王击球时球的最小速度为 $4 \sqrt{15} \mathrm{~m} / \mathrm{s}$
如图所示为某款手机充电器,其铭牌标识如下:“输入:AC、220V、50Hz”,“输出:DC、3V、6V、9V、12V”,“电流:1000mA 1500mA”,该充电器正常工作时,下列说法正确的是

$\text{A.}$ 输入电压的最大值为220V,频率为50Hz
$\text{B.}$ 充电器输出功率的变化范围为3W 18W
$\text{C.}$ 充电器内部变压器的原线圈匝数小于副线圈匝数
$\text{D.}$ 充电器内部变压器输入电压的频率大于输出电压的频率
一同学将铅球水平推出,不计空气阻力和转动的影响,铅球在平抛运动过程中
$\text{A.}$ 机械能一直增加
$\text{B.}$ 加速度保持不变
$\text{C.}$ 速度大小保持不变
$\text{D.}$ 被推出后瞬间动能最大