单选题 (共 6 题 ),每题只有一个选项正确
函数$f(x)=\dfrac{sin x+x}{cos x+x^2}$ 在$[-\pi,\pi]$的图像大致为
$\text{A.}$  $\text{B.}$
$\text{B.}$ 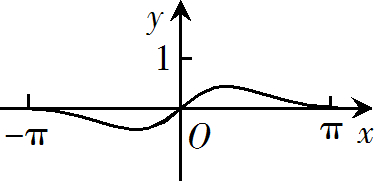 $\text{C.}$
$\text{C.}$ 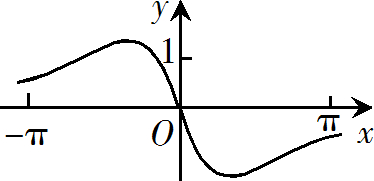 $\text{D.}$
$\text{D.}$ 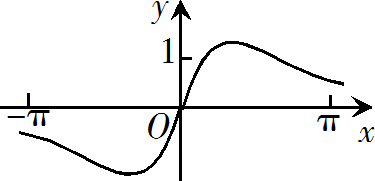
如图是求 $ \frac{1}{2+\frac{1}{2+\frac{1}{2}}} $ 的程序框图, 图中空白框中应填入 ( )
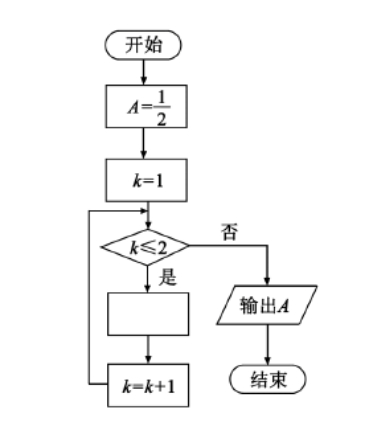
$\text{A.}$ $A=\frac{1}{2+A}$
$\text{B.}$ $A=2+\frac{1}{A}$
$\text{C.}$ $A=\frac{1}{1+2 A}$
$\text{D.}$ $A=1+\frac{1}{2 A}$
已知椭圆的焦点为 $ F_{1}(-1,0)$,$ F_{2}(1,0)$ , 过$F_{2}$ 的直线与 C 交于 A, B 两点. 若 $\left|A F_{2}\right|=2\left|F_{2} B\right| $ ,$|AB|=|BF_1|$, 则C的方程为 ( )
$\text{A.}$ $\frac{x^{2}}{2}+y^{2}=1$
$\text{B.}$ $\frac{x^{2}}{3}+\frac{y^{2}}{2}=1$
$\text{C.}$ $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$
$\text{D.}$ $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$
已知三棱锥 P−ABC 的四个顶点在球 O 的球面上,PA=PB=PC,△ABC 是边长为 2 的正三角形,E,F 分别是 PA,AB 的中点,∠CEF=90°,则球 O 的体积为
$\text{A.}$ $8 \sqrt{6} \pi$
$\text{B.}$ $4 \sqrt{6} \pi$
$\text{C.}$ $2 \sqrt{6} \pi$
$\text{D.}$ $ \sqrt{6} \pi$
在正方体 $A B C D-A_{i} B_{i} C_{:} D_{i}$ 中, $P$ 为 $B_{i} D_{i}$ 的中点, 则直线 $P B$ 与 $A D_{i}$ 所成的角为 ( )
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{6}$
把函数 $y=f(x)$ 图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍, 纵坐标不变, 再把所 得曲线向右平移 $\frac{\pi}{3}$ 个单位长度, 得到函数 $y=\sin \left(x-\frac{\pi}{4}\right)$ 的图像, 则 $f(x)=$ ( )
$\text{A.}$ $\sin \left(\frac{x}{2}-\frac{7 \pi}{12}\right)$
$\text{B.}$ $\sin \left(\frac{x}{2}+\frac{\pi}{12}\right)$
$\text{C.}$ $\sin \left(2 x-\frac{7 \pi}{12}\right)$
$\text{D.}$ $\sin \left(2 x+\frac{\pi}{12}\right)$