一、单选题 （共 29 题，每小题 5 分，共 50 分，每题只有一个选项正确）
图1是第七届国际数学教育大会(ICME) 会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC ．若 $AB=BC=1, \angle A O B=\alpha$，则 $OC^2$ 的值为 （ ）
$\text{A.}$ $\frac{1}{\sin ^{2} \alpha}+1$
$\text{B.}$ $\sin ^{2} \alpha+1$
$\text{C.}$ $\frac{1}{\cos ^{2} \alpha}+1$
$\text{D.}$ $\cos ^{2} \alpha+1$
若菱形的周长为16，高为2，则菱形两邻角的度数之比为（ ）
$\text{A.}$ 4:1
$\text{B.}$ 5:1
$\text{C.}$ 6:1
$\text{D.}$ 7:1
已知点 $A, B, C$ 在 $\odot O$ 上, 则下列命题为真命题的是 ( )
$\text{A.}$ 若半径 $O B$ 平分弦 $A C$, 则四边形 $O A B C$ 是平行四边形
$\text{B.}$ 若四边形 $O A B C$ 是平行四边形, 则 $\angle A B C=120^{\circ}$
$\text{C.}$ 若 $\angle A B C=120^{\circ}$, 则弦 $A C$ 平分半径 $O B$
$\text{D.}$ 若弦 $A C$ 平分半径 $O B$, 则半径 $O B$ 平分弦 $A C$
若一个正方形的面积是 12 , 则它的边长是（ ）
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ 3
$\text{C.}$ $3 \sqrt{2}$
$\text{D.}$ 4
如图, 在菱形 $A B C D$ 中, $A B=2, \angle A=120^{\circ}$, 过菱形 $A B C D$ 的对称中心 $O$ 分别作边 $A B$, $B C$ 的垂线, 交各边于点 $E, F, G, H$, 则四边形 $E F G H$ 的周长为
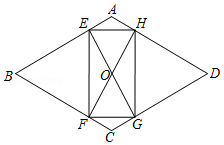
$\text{A.}$ $3+\sqrt{3}$
$\text{B.}$ $2+2 \sqrt{3}$
$\text{C.}$ $2+\sqrt{3}$
$\text{D.}$ $1+2 \sqrt{3}$
如图, 在 $\square A B C D$ 中, 一定正确的是（）
$\text{A.}$ $A D=C D$
$\text{B.}$ $A C=B D$
$\text{C.}$ $A B=C D$
$\text{D.}$ $C D=B C$
如图, 平行四边形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $O$. 点 $E$ 为 $B C$ 的中点, 连接 $E O$ 并延长交 $A D$ 于点 $F, \angle A B C=60^{\circ}, B C=2 A B$. 下列结论：(1) $A B \perp A C$ : (2) $A D=4 O E$ : (3)四边形 $A E C F$ 是菱形: (4) $S_{\triangle B O E}=\frac{1}{4} S_{\triangle A B C}$ 、其中正确结论的个数是
$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 1
如图, 四边形 $A B C D$ 为矩形， $A B=3, B C=4$. 点 $P$ 是线段 $B C$ 上一动点, 点 $M$ 为线段 $A P$ 上一 点. $\angle A D M=\angle B A P$, 则 $B M$ 的最小值为 ( )
$\text{A.}$ $\frac{5}{2}$
$\text{B.}$ $\frac{12}{5}$
$\text{C.}$ $\sqrt{13}-\frac{3}{2}$
$\text{D.}$ $\sqrt{13}-2$
如图, 在菱形 $A B C D$ 中, 点 $E 、 F$ 分别是边 $B C 、 C D$ 的中点, 连 接 $A E 、 A F 、 E F$. 若菱形 $A B C D$ 的面积为 8, 则 $\triangle A E F$ 的面积为（）
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
下列说法错误的是
$\text{A.}$ 对角线垂直且互相平分的四边形是菱形
$\text{B.}$ 同圆或等圆中, 同弧对应的圆周角相等
$\text{C.}$ 对角线相等的四边形是矩形
$\text{D.}$ 对角线垂直且相等的四边形是正方形
如图, 在平行四边形 $A B C D$ 中, $A D=2 A B=2, \angle A B C=60^{\circ}, E, F$ 是对角线 $B D$ 上的动点, 且 $B E=D F, M, N$ 分别是边 $A D$, 边 $B C$ 上的动点. 下列四种说法:
(1)存在无数个平行四边形 MENF；
(2)存在无数个矩形 $M E N F$;
(3)存在无数个菱形 $M E N F$ ；
(4)存在无数个正方形 MENF.
其中正确的个数是（）
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如图, 菱形 $A B C D$ 的顶点分别在反比例函数 $y=\frac{2}{x}$ 和 $y=-\frac{5}{x}$ 的 图象上, 且边长为 $\sqrt{7}$, 则菱形 $A B C D$ 的面积为
$\text{A.}$ $2 \sqrt{10}$
$\text{B.}$ $4 \sqrt{10}$$4 \sqrt{10}$
$\text{C.}$ $2 \sqrt{7}$
$\text{D.}$ $4 \sqrt{7}$
如图, 在菱形 $A B C D$ 中, 对角线 $A C, B D$ 相交于点 $O$, 点 $E$ 为 $C D$ 的中点. 若 $O E=3$, 则菱形 $A B C D$ 的周长为
$\text{A.}$ 6
$\text{B.}$ 12
$\text{C.}$ 24
$\text{D.}$ 48
如图, 在正方形 $A B C D$ 中, $A E$ 平分 $\angle B A C$ 交 $B C$ 于点 $E$, 点 $F$ 是边 $A B$ 上一点, 连接 $D F$, 若 $B E=A F$, 则 $\angle C D F$ 的度数为 ( )
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $67.5^{\circ}$
$\text{D.}$ $77.5^{\circ}$
若顺次连接四边形 $A B C D$ 各边的中点所得的四边形是正方形, 则四边形 $A B C D$ 的两条对角线 $A C, B D$ 一定是 ( )
$\text{A.}$ 互相平分
$\text{B.}$ 互相垂直
$\text{C.}$ 互相平分且相等
$\text{D.}$ 互相垂直且相等
如图, 点 $O$ 是菱形 $A B C D$ 对角线 $A C$ 的中点, 过 $O$ 作 $O H \perp A B$ 于 $H$. 若 $A B=5$, $A C=8$, 则 $O H$ 的长为 ( )
$\text{A.}$ $2$
$\text{B.}$ $2.4$
$\text{C.}$ $2.5$
$\text{D.}$ $3$
如图, 证明矩形的对角线相等. 已知: 四边形 $A B C D$ 是矩形. 求证: $A C=B D$. 以 下是排乱的证明过程: ① $\therefore A B=C D, \angle A B C=\angle D C B$; ②$\because B C=C B$;③ $\because$ 四边形 $A B C D$ 是矩形;④ $\therefore A C=D B$; ⑤$\therefore \triangle A B C \cong \triangle D C B$.
甲的证明顺序是：(3)(1)(2)(5)(4)
乙的证明顺序是: (2)(3)(1)(5) (4)
则下列说法正确的是（）
$\text{A.}$ 甲和乙都对
$\text{B.}$ 甲和乙都不对
$\text{C.}$ 甲对乙不对
$\text{D.}$ 乙对甲不对
如图, 在平面直角坐标系中有菱形 $O A B C$, 点 $A$ 的坐标为 $(5,0)$, 对角线 $O B 、 A C$ 相交于 点 $D$, 双曲线 $y=\frac{k}{x}(x>0)$ 经过 $A B$ 的中点 $F$, 交 $B C$ 于点 $E$, 且 $O B \cdot A C=40$, 下列四 个结论: (1)双曲线的解析式为 $y=\frac{7}{x}(x>0)$; (2) $E$ 点的坐标是 $\left(\frac{7}{4}, 4\right)$; (3) $\sin \angle C A O=\frac{\sqrt{5}}{5}$; (4) $A C+O B=6 \sqrt{5}$. 其中正确的结论有
$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3 个
$\text{D.}$ 4 个
如图, 在正方形 $A B C D$ 中, 点 $G$ 是 $B C$ 上一点, 且 $\frac{G C}{B G}=\frac{1}{2}$, 连接 $D G$ 交对角线 $A C$ 于 $F$ 点, 过 $D$ 点作 $D E \perp D G$ 交 $C A$ 的延长线于点 $E$, 若 $A E=3$, 则 $D F$ 的长为
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $\frac{4 \sqrt{5}}{3}$
$\text{C.}$ $\frac{9}{2}$
$\text{D.}$ $\frac{3 \sqrt{5}}{2}$
如图 5, 在矩形 $A B C D$ 中, $A D>A B$, 点 $E, F$ 分别在 $A D, B C$ 边上, $E F / / A B, A E=A B, A F$ 与 $B E$ 相交于点 $O$, 连接 $O C$. 若 $B F=2 C F$, 则 $O C$ 与 $E F$ 之间的数量关系正确的是
$\text{A.}$ $2 O C=\sqrt{5} E F$
$\text{B.}$ $\sqrt{5} O C=2 E F$
$\text{C.}$ $2 O C=\sqrt{3} E F$
$\text{D.}$ $O C=E F$
如图, 四边形 $A B C D$ 的对角线 $A C \perp B D$ 于点 $O$, 点 $E, F, G, H$ 分别为边 $A B$, $B C, C D$ 和 $A D$ 的中点, 顺次连接 $E F, F G, G H$ 和 $H E$ 得到四边形 $E F G H$. 若 $A C=10, B D=8$, 则四边形 $E F G H$ 的面积等于
$\text{A.}$ 45
$\text{B.}$ 40
$\text{C.}$ 20
$\text{D.}$ 18
如图, 在平面直角坐标系 $x O \mathrm{y}$ 中, 矩形 $O A B C$ 的顶点 $\mathrm{B}$ 的坐标为 $(10,4)$, 四边形 $\mathrm{ABEF}$ 是菱形, 且 $\tan \angle \mathrm{ABE}=\frac{4}{3}$. 若直线 $l$ 把矩形 $O \mathrm{ABC}$ 和菱形 $\mathrm{ABEF}$ 组成的图形的面积 分成相等的两部分, 则直线 $l$ 的解析式为
$\text{A.}$ $y=3 x$
$\text{B.}$ $y=-\frac{3}{4} x+\frac{15}{2}$
$\text{C.}$ $y=-2 x+11$
$\text{D.}$ $y=-2 x+12$
如图，等边 $\triangle A B C$ 钢架的立柱 $C D \perp A B$ 于点 $\mathrm{D} ， A B$ 长 $12 \mathrm{~m}$. 现将钢架立柱缩短成 $D E ， \angle B E D=60^{\circ}$. 则新钢架减少用钢
$\text{A.}$ $(24-12 \sqrt{3}) \mathrm{m}$
$\text{B.}$ $(24-8 \sqrt{3}) \mathrm{m}$
$\text{C.}$ $(24-6 \sqrt{3}) \mathrm{m}$
$\text{D.}$ $(24-4 \sqrt{3}) \mathrm{m}$
若两个相似三角形的相似比是 $1: 3$ ，则这两个相似三角形的面积比是
$\text{A.}$ $1: 3$
$\text{B.}$ $1: 4$
$\text{C.}$ $1: 6$
$\text{D.}$ $1: 9$
如图, 在 $R t \triangle A B C$ 中, $A C=B C=2$, 点 $D$ 在 $A B$ 的延长线上, 且 $C D=A B$, 则 $B D$ 的长是
$\text{A.}$ $\sqrt{10}-\sqrt{2}$
$\text{B.}$ $\sqrt{6}-\sqrt{2}$
$\text{C.}$ $2 \sqrt{2}-2$
$\text{D.}$ $2 \sqrt{2}-\sqrt{6}$
在凸五边形 $A B C D E$ 中, $A B=A E, B C=D E, F$ 是 $C D$ 的中点. 下列条件中, 不能推出 $A F$ 与 $C D$ 一定垂直的是
$\text{A.}$ $\angle A B C=\angle A E D$
$\text{B.}$ $\angle B A F=\angle E A F$
$\text{C.}$ $\angle B C F=\angle E D F$
$\text{D.}$ $\angle A B D=\angle A E C$
下列条件中, 不能判定 $\triangle A B C \cong \triangle A^{\prime} B^{\prime} C^{\prime}$ 的是
$\text{A.}$ $\angle \mathrm{A}=\angle \mathrm{A}, \angle \mathrm{C}=\angle \mathrm{C}, \mathrm{AC}=\mathrm{A}^{\prime} \mathrm{C}^{\prime}$
$\text{B.}$ $\angle \mathrm{C}=\angle \mathrm{C}^{\prime}=90^{\circ}, \mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
$\text{C.}$ $\angle \mathrm{A}=\angle \mathrm{A}^{\prime}=80^{\circ}, \angle \mathrm{B}=60^{\circ}, \angle \mathrm{C}^{\prime}=40^{\circ}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
$\text{D.}$ $\angle \mathrm{A}=\angle \mathrm{A}, \mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
如图, 锐角三角形 $A B C$ 中, $A B=A C$, 点 $D, E$ 分别在边 $A B, A C$ 上,连接 $B E, C D$. 下列命题中, 假命题是
$\text{A.}$ 若 $C D=B E$, 则 $\angle D C B=\angle E B C$
$\text{B.}$ 若 $\angle D C B=\angle E B C$, 则 $C D=B E$
$\text{C.}$ 若 $B D=C E$, 则 $\angle D C B=\angle E B C$
$\text{D.}$ 若 $\angle D C B=\angle E B C$, 则 $B D=C E$
如图, 在 $\triangle A B C$ 中, $D$ 是边 $B C$ 上的点 (不与点 $B, C$ 重合). 过点 $D$作 $D E / / A B$ 交 $A C$ 于点 $E$; 过点 $D$ 作 $D F / / A C$ 交 $A B$ 于点 $F 、 N$ 是线段 $B F$ 上的点, $B N=2 N F: M$ 是线段 $D E$ 上的点, $D M=2 M E$. 若已知 $\triangle C M N$ 的面积, 则一定能求出
$\text{A.}$ $\triangle A F E$ 的面积
$\text{B.}$ $\triangle B D F$ 的面积
$\text{C.}$ $\triangle B C N$ 的面积
$\text{D.}$ $\triangle D C E$ 的面积
二、填空题 （共 28 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
图1是邻边长为$2$和$6$的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2) ，则图1中所标注的d的值为 （ ）；记图1中小正方形的中心为点$A,B,C$ 图2中的对应点为点$A',B'C,$．以大正方形的中心$O$为圆心作圆，则当点$A',B',C'$ 在圆内或圆上时，圆的最小面积为 （ ）
如图，在菱形ABCD中，对角线AC、BD相交于点O，点E在线段BO上，连接AE，若CD＝2BE，∠DAE＝∠DEA，EO＝1，则线段AE的长为 （ ）
如图, 在Y $A B C D$ 中, 对角线 $A C, B D$ 交于点 $O, A B \perp A C, A H \perp B D$ 于点 $H$, 若 $A B=2$, $B C=2 \sqrt{3}$, 则 $A H$ 的长为 （ ）
如图, 在矩形 $A B C D$ 中, 点 $E, F$ 分别在 $B C, A D$ 上, $A F=E C$. 只 需添加一个条件即可证明四边形 $A E C F$ 是菱形, 这个条件可以是 (写出一个即可).
如图, 在矩形 $A B C D$ 中, $E$ 是 $B C$ 边上一点, $\angle A E D=90^{\circ}, \angle E A D=30^{\circ}$, $F$ 是 $A D$ 边的中点, $E F=4 \mathrm{~cm}$, 则 $B E=$
如图, 在 $\square A B C D$ 中, $A D=5, A B=12, \sin A=\frac{4}{5}$. 过点 $D$ 作 $D E \perp A B$, 垂足为 $E$, 则 $\sin \angle B C E=$
如图所示, 在口 $A B C D$ 中, $A C, B D$ 交于点 $O, \overrightarrow{B O}=\vec{a}, \overrightarrow{B C}=\vec{b}$, 则 $\overrightarrow{D C}=$
如图, 在矩形 $A B C D$ 中, 若 $A B=3, A C=5, \frac{\mathrm{AF}}{\mathrm{FC}}=\frac{1}{4}$, 则 $A E$ 的长为
如图, 四边形 $A B C D$ 为平行四边形, 则点 $B$ 的坐标为
如图, 四边形 $A B C D$ 为正方形, 点 $E$ 是 $B C$ 的中点, 将正方形 $A B C D$ 沿 $A E$ 折叠, 得到点 $B$ 的对应 点为点 $F$, 延长 $E F$ 交线段 $D C$ 于点 $P$, 若 $A B=6$, 则 $D P$ 的长度为
