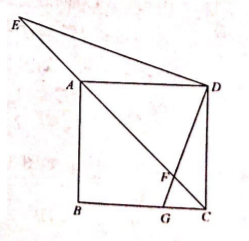
如图, 在正方形 $A B C D$ 中, 点 $G$ 是 $B C$ 上一点, 且 $\frac{G C}{B G}=\frac{1}{2}$, 连接 $D G$ 交对角线 $A C$ 于 $F$ 点, 过 $D$ 点作 $D E \perp D G$ 交 $C A$ 的延长线于点 $E$, 若 $A E=3$, 则 $D F$ 的长为
A
$2 \sqrt{2}$
B
$\frac{4 \sqrt{5}}{3}$
C
$\frac{9}{2}$
D
$\frac{3 \sqrt{5}}{2}$
E
F