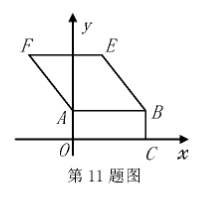
如图, 在平面直角坐标系 $x O \mathrm{y}$ 中, 矩形 $O A B C$ 的顶点 $\mathrm{B}$ 的坐标为 $(10,4)$, 四边形 $\mathrm{ABEF}$ 是菱形, 且 $\tan \angle \mathrm{ABE}=\frac{4}{3}$. 若直线 $l$ 把矩形 $O \mathrm{ABC}$ 和菱形 $\mathrm{ABEF}$ 组成的图形的面积 分成相等的两部分, 则直线 $l$ 的解析式为
A
$y=3 x$
B
$y=-\frac{3}{4} x+\frac{15}{2}$
C
$y=-2 x+11$
D
$y=-2 x+12$
E
F