一、单选题 （共 44 题，每小题 5 分，共 50 分，每题只有一个选项正确）
已知 $\alpha \in\left(-\frac{\pi}{2}, 0\right)$, 且 $\tan \left(\frac{\pi}{4}-\alpha\right)=3 \cos 2 \alpha$, 则 $\sin 2 \alpha=$
$\text{A.}$ $-\frac{1}{6}$
$\text{B.}$ $-\frac{1}{3}$
$\text{C.}$ $-\frac{2}{3}$
$\text{D.}$ $-\frac{5}{6}$
已知角 $\alpha$ 的顶点与原点重合, 始边与 $x$ 轴正半轴重合, 终边经过点 $(1,-2)$, 则 $\tan 2 \alpha=$
$\text{A.}$ $-\frac{3}{4}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $-\frac{4}{3}$
$\text{D.}$ $\frac{4}{3}$
已知 $\tan \left(\theta+\frac{\pi}{4}\right)=\frac{1}{2} \tan \theta-\frac{7}{2}$, 则 $\cos 2 \theta=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{4}{5}$
$\text{D.}$ $\frac{4}{5}$
已知函数 $f(x)=\cos ^2 x+\sin x \cos x-\frac{1}{2}$ 的图象为 $C$, 以下说法中正确的是
$\text{A.}$ 函数 $f(x)$ 的最大值为 $\frac{\sqrt{2}+1}{2}$
$\text{B.}$ 图象 $C$ 相邻两条对称轴的距离为 $\frac{\pi}{2}$
$\text{C.}$ 图象 $C$ 关于 $\left(-\frac{\pi}{8}, 0\right)$ 中心对称
$\text{D.}$ 要得到函数 $y=\frac{\sqrt{2}}{2} \sin x$ 的图象, 只需将函数 $f(x)$ 的图象横坐标伸长为原来的 2 倍, 再向右平移 $\frac{\pi}{4}$ 个单位
已知 $\alpha, \beta$ 为锐角, $\tan \alpha=\frac{4}{3}, \cos (\alpha+\beta)=-\frac{\sqrt{5}}{5}$, 则 $\tan (\alpha-\beta)=$
$\text{A.}$ -2
$\text{B.}$ $-\frac{24}{7}$
$\text{C.}$ $-\frac{\sqrt{5}}{5}$
$\text{D.}$ $-\frac{2}{11}$
若函数 $f(x)=\sin \left(\omega_X+\phi\right)\left(\omega>0, | \phi| < \frac{\pi}{2} \right) $ 的部分图象如图所示, $A\left(\frac{\pi}{3}, 0\right), B\left(\frac{7 \pi}{12},-1\right)$ ，则 $f(x)$ 的解析式是
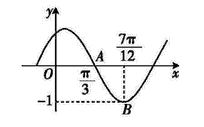
$\text{A.}$ $f(x)=\sin \left(x+\frac{\pi}{6}\right)$
$\text{B.}$ $f(x)=\sin \left(x \frac{\pi}{6}\right)$
$\text{C.}$ $f(x)=\sin \left(2 x+\frac{\pi}{3}\right)$
$\text{D.}$ $f(x)=\sin \left(2 x-\frac{\pi}{6}\right)$
将函数 $y=\frac{1}{2} \sin x+x\left(x \in\left[0, \frac{\pi}{2}\right]\right)$ 的图象绕着原点沿逆时针方向旋转 $\theta$ 角得到曲线 $\Gamma$, 已知曲线 $\Gamma$ 始终保持为函数图象, 则 $\tan \theta$ 的最大值为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ 1
$\text{D.}$ $\frac{3}{2}$
设函数 $f(x)=\cos \left(\omega x+\frac{\pi}{6}\right)-2(\omega>0)$ 的导函数 $f^{\prime}(x)$ 的最大值为 2 , 则 $f(x)$ 在 $\left[-\frac{\pi}{6}, \frac{\pi}{2}\right]$ 上的最小值为
$\text{A.}$ $\frac{\sqrt{3}}{2}-2$
$\text{B.}$ $-\frac{5}{2}$
$\text{C.}$ $-\frac{\sqrt{3}}{2}-2$
$\text{D.}$ $-3$
已知 $\alpha, \beta \in\left(0, \frac{\pi}{4}\right), \sin \alpha \cos \left(\frac{3 \pi}{2}+\alpha\right)-\sin \left(\frac{\pi}{2}+\alpha\right) \cos \alpha=-\frac{3}{5}$, 且 $3 \sin \beta=\sin (2 \alpha+\beta)$,则 $\alpha+\beta$ 的值为
$\text{A.}$ $\frac{\pi}{12}$
$\text{B.}$ $\frac{\pi}{6}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{3}$
若点 $P\left(\sin \frac{\pi}{6}, \frac{1}{2}\right)$ 在角 $\alpha$ 的终边上, 则 $\tan \alpha$ 的值为
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ 1
$\text{C.}$ $\frac{\pi}{6}$
$\text{D.}$ $\frac{\pi}{4}$
已知扇形 $O A B$ 的面积为 $\pi, \overparen{A B}$ 的长为 $\pi$, 则 $A B=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $2 \sqrt{2}$
$\text{D.}$ 4
已知角 $\alpha$ 的终边与角 $\beta$ 的终边关于 $y=x$ 对称 ( $\beta$ 为象限角), 则 $\frac{\cos (\alpha-\beta)}{\sin 2 \beta}=$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 2
若定义在$\mathbf{R}$上的函数$f(x)=\sin\omega x+\cos\omega x(\omega>0)$的图象在区间$[0,\pi]$上恰有5条对称轴，则$\omega$的取值范围为
$\text{A.}$ $\left[\dfrac{17}{4},\dfrac{21}{4}\right)$
$\text{B.}$ $\left(\dfrac{17}{4},\dfrac{25}{4}\right)$
$\text{C.}$ $\left[\dfrac{17}{4},\dfrac{25}{4}\right)$
$\text{D.}$ $\left[\dfrac{33}{4},\dfrac{41}{4}\right)$
已知 $\theta \in\left(\frac{3 \pi}{4}, \pi\right), \tan 2 \theta=-4 \tan \left(\theta+\frac{\pi}{4}\right)$, 则 $\frac{1+\sin 2 \theta}{2 \cos ^2 \theta+\sin 2 \theta}=$
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ 1
$\text{D.}$ $\frac{3}{2}$
已知 $f(x)=A \sin (\omega x+\varphi)(A>0, \omega>0,|\varphi| < \pi)$ 的部分图象如图所示, 则
$\text{A.}$ $f(x)=\sin \left(2 x+\frac{3 \pi}{4}\right)$
$\text{B.}$ $f(x)$ 的图象的一个对称中心为 $\left(\frac{\pi}{8}, 0\right)$
$\text{C.}$ $f(x)$ 的单调递增区间是 $\left[\frac{\pi}{8}+k \pi, \frac{5 \pi}{8}+k \pi\right], k \in \mathbf{Z}$
$\text{D.}$ 把 $f(x)$ 的图象向左平移 $\frac{5 \pi}{8}$ 个单位后得到的是一个奇函数的图象
试问有多少个实数 $x$ 满足 $\sin \left(x+\frac{\pi}{6}\right)=\sin x+\sin \frac{\pi}{6}$ 且 $0 \leq x < 2 \pi$ ?
$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3个
$\text{D.}$ 4个
在同一平面上, 相距 7 公里的 $A 、 B$ 两炮台, $A$ 在 $B$ 的正东方。某次演习时, $A$ 向西偏北 $\theta$ 方向发射炮弹, $B$ 则向东偏北 $\theta$ 方向发射砲弹, 其中 $\theta$ 为锐角, 观测回报两炮弹皆命中 9 公里外的同一目标 $P$ 。接著 $A$ 改向西偏北 $\frac{\theta}{2}$ 方向发射炮弹，弹著点为 9 公里外的点 $Q$ ，试问炮弹$B$与弹著点$Q$的距离$BQ$为何?
$\text{A.}$ 4 公里
$\text{B.}$ 4.5 公里
$\text{C.}$ 5 公里
$\text{D.}$ 5.5 公里
已知函数 $f(x)=\left\{\begin{array}{l}\sin x, x \leq 0 \\ f\left(x-\frac{\pi}{2}\right)+m, x>0\end{array}\right.$ 满足 $f(\pi)=1$, 则实数 $m$ 的值为
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
已知函数 $f(x)=\sin \pi x, x \in(0,2)$ 的图象与直线 $y=a(x-1)$ 有 3 个交点, 则实数 $a$ 的取值范围为
$\text{A.}$ $(-\infty, 0)$
$\text{B.}$ $(-1,0)$
$\text{C.}$ $(-\infty,-\pi)$
$\text{D.}$ $(-\pi, 0)$
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $\frac{a-b}{c-b}=$ $\frac{\sin C}{\sin A+\sin B}$, 则 $A=$
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{\pi}{3}$ 或 $\frac{2 \pi}{3}$
在锐角 $\triangle A B C$ 中, 角 $A, B, C$ 所对应的边分别为 $a, b, c$, 若 $b$ $=2 a \sin B$, 则角 $A$ 等于
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $30^{\circ}$ 或 $150^{\circ}$
在 $\triangle A B C$ 中, $B C=3, \sin B+\sin C=\frac{\sqrt{10}}{3} \sin A$, 且 $\triangle A B C$ 的面积为 $\frac{1}{2} \sin A$, 则 $A=$
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{2 \pi}{3}$
记 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $(a+b+c)(b+c-a)=2 b c$, 那么 $\triangle A B C$ 是
$\text{A.}$ 锐角三角形
$\text{B.}$ 直角三角形
$\text{C.}$ 钝角三角形
$\text{D.}$ 无法确定
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $\frac{c^2-a^2-b^2}{2 a b}>0$, 则 $\triangle A B C$ 一定是
$\text{A.}$ 锐角三角形
$\text{B.}$ 直角三角形
$\text{C.}$ 针角三角形
$\text{D.}$ 等边三角形
在 $\triangle A B C$ 中, $a, b, c$ 分别为三个内角 $A, B, C$ 的对边, 若 $a=2, b=1, B=29^{\circ}$, 则此三角形解的情况是
$\text{A.}$ 无解
$\text{B.}$ 有一解
$\text{C.}$ 有两解
$\text{D.}$ 有无数解
在 $\triangle A B C$ 中, 已知 $a=18, b=20, A=150^{\circ}$, 这个三角形解的情况是
$\text{A.}$ 一解
$\text{B.}$ 两解
$\text{C.}$ 无解
$\text{D.}$ 不确定
记 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $a \sin B=b \sin C$, 则 $\triangle A B C$ 的面积为
$\text{A.}$ $\frac{a^2 \sin 2 C}{2}$
$\text{B.}$ $\frac{b^2 \sin 2 A}{2}$
$\text{C.}$ $\frac{c^2 \sin 2 B}{2}$
$\text{D.}$ $\frac{\sqrt{3}\left(a^2+b^2+c^2\right)}{12}$
) 在 $\triangle A B C$ 中, 角 $A, B, C$ 所对应的边分别为 $a, b, c$, 设 $\triangle A B C$ 的面积为 $S$, 则 $\frac{S}{a^2+4 b c}$ 的最大值为
$\text{A.}$ $\frac{\sqrt{2}}{16}$
$\text{B.}$ $\frac{\sqrt{3}}{12}$
$\text{C.}$ $\frac{\sqrt{3}}{16}$
$\text{D.}$ $\frac{\sqrt{2}}{18}$
锐角 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 若 $a^2+b^2=5 c^2$, 则 $\cos C$的取值范围是
$\text{A.}$ $\left(\frac{1}{2}, \frac{\sqrt{6}}{3}\right)$
$\text{B.}$ $\left(\frac{1}{2}, 1\right)$
$\text{C.}$ $\left[\frac{4}{5}, \frac{\sqrt{6}}{3}\right)$
$\text{D.}$ $\left[\frac{4}{5}, 1\right)$
在锐角三角形 $A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 且满足 $\frac{a}{2}+a \cos B=\frac{c}{2}$, 则 $\frac{\tan B-\tan A}{2 \tan A \cdot \tan B}$ 的取值范围是
$\text{A.}$ $\left(\frac{1}{2}, \frac{\sqrt{3}}{3}\right)$
$\text{B.}$ $\left(\frac{\sqrt{3}}{4}, \frac{1}{2}\right)$
$\text{C.}$ $\left(0, \frac{1}{2}\right)$
$\text{D.}$ $\left(1, \frac{2 \sqrt{3}}{3}\right)$
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c, A=60^{\circ}, b=3 c$, 角 $A$的平分线交 $B C$ 于点 $D$, 且 $B D=\sqrt{7}$, 则 $\cos \angle A D B$ 的值为
$\text{A.}$ $-\frac{\sqrt{21}}{7}$
$\text{B.}$ $\frac{\sqrt{21}}{7}$
$\text{C.}$ $\frac{2 \sqrt{7}}{7}$
$\text{D.}$ $\pm \frac{\sqrt{21}}{7}$
已知点 $G$ 为三角形 $A B C$ 的重心, 且 $|\overrightarrow{G A}+\overrightarrow{G B}|=|\overrightarrow{G A}-\overrightarrow{G B}|$, 当 $\angle C$ 取最大值时, $\cos C=$
$\text{A.}$ $\frac{4}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{1}{5}$
已知 $\alpha, \beta \in\left(0, \frac{\pi}{2}\right), 2 \tan \alpha=\frac{\sin 2 \beta}{\sin \beta+\sin ^2 \beta}$, 则 $\tan \left(2 \alpha+\beta+\frac{\pi}{3}\right)=$
$\text{A.}$ $-\sqrt{3}$
$\text{B.}$ $-\frac{\sqrt{3}}{3}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\sqrt{3}$
已知函数 $f(x)=\frac{\cos x}{x}$, 若 ${A}, B$ 是锐角 $\triangle A B C$ 的两个内角, 则下列结论一定正确的是
$\text{A.}$ $f(\sin A)>f(\sin B)$
$\text{B.}$ $f(\cos A)>f(\cos B)$
$\text{C.}$ $f(\sin A)>f(\cos B)$
$\text{D.}$ $f(\cos A)>f(\sin B)$
已知函数 $f(x)=\cos 2 x, g(x)=\sin x$, 则存在 $\theta \in\left(\frac{\pi}{6}, \frac{\pi}{4}\right)$, 使得
$\text{A.}$ $2 g(\theta)=f(\theta)+g(\theta) \cdot f(\theta)$
$\text{B.}$ $4 g(\theta) \cdot f(\theta)=f(\theta)+2 g(\theta)$
$\text{C.}$ $2 f(\theta)=g(\theta)+g(\theta) \cdot f(\theta)$
$\text{D.}$ $f(\theta)=g(\theta)$
函数 $y=2 \tan \left(3 x+\frac{\pi}{6}\right)$ 的定义域是
$\text{A.}$ $\left\{x \left\lvert\, x \neq \frac{\pi}{2}+k \pi\right., k \in \mathrm{Z}\right\}$
$\text{B.}$ $\left\{x \left\lvert\, x \neq \frac{\pi}{12}+k \pi\right., k \in \mathrm{Z}\right\}$
$\text{C.}$ $\left\{x \left\lvert\, x \neq \frac{\pi}{6}+\frac{k \pi}{3}\right., k \in Z\right\}$
$\text{D.}$ $\left\{x \left\lvert\, x \neq \frac{\pi}{9}+\frac{k \pi}{3}\right., k \in \mathrm{Z}\right\}$
已知 $\tan \alpha=3$, 则 $\frac{\sin (\pi-\alpha)+2 \cos (\pi+\alpha)}{\sin \left(\frac{\pi}{2}+\alpha\right)+\cos \left(\frac{3 \pi}{2}+\alpha\right)}=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{5}{4}$
$\text{D.}$ $\frac{1}{2}$
已知 $\cos \left(140^{\circ}-\alpha\right)+\sin \left(110^{\circ}+\alpha\right)=\sin \left(130^{\circ}-\alpha\right)$, 求 $\tan \alpha=$
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $-\frac{\sqrt{3}}{3}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $-\sqrt{3}$
已知 $x \in\left[0, \frac{\pi}{4}\right], \sin x+\cos x=\frac{3 \sqrt{5}}{5}$, 则 $\tan \left(x-\frac{3 \pi}{4}\right)=$.
$\text{A.}$ 3
$\text{B.}$ -3
$\text{C.}$ $-\sqrt{5}$
$\text{D.}$ 2
求值: $2 \sin 80^{\circ} \cos 20^{\circ}-\frac{\sin 20^{\circ}}{2 \sin 10^{\circ}}=$
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $1$
$\text{D.}$ $\frac{\sqrt{3}}{2}$