单选题 (共 8 题 ),每题只有一个选项正确
记集合 $M=\left\{x \mid x^2>4\right\}, N=\left\{x \mid x^2-4 x \leqslant 0\right\}$, 则 $M \cap N=$
$\text{A.}$ $\{x \mid 2 < x \leqslant 4\}$
$\text{B.}$ $\{x \mid x \geqslant 0$ 或 $x < -2\}$
$\text{C.}$ $\{x \mid 0 \leqslant x < 2\}$
$\text{D.}$ $\{x \mid-2 < x \leqslant 4\}$
已知 $f(x), g(x)$ 分别是定义在 $\mathbf{R}$ 上的偶函数和奇函数, 且 $f(x)-$ $g(x)=x^3+x^2+1$, 则 $f(1)+g(1)=$
$\text{A.}$ $-3$
$\text{B.}$ $-1$
$\text{C.}$ $1$
$\text{D.}$ $3$
已知向量 $\boldsymbol{a}=(-1,2)$, 点 $A(-2,1)$, 若 $\overrightarrow{A B} / / \boldsymbol{a}$ 且 $|\overrightarrow{A B}|=3 \sqrt{5}, O$ 为坐 标原点, 则 $\overrightarrow{O B}$ 的坐标为
$\text{A.}$ $(1,-5)$
$\text{B.}$ $(-5,7)$
$\text{C.}$ $(1,-5)$ 或 $(5,-7)$
$\text{D.}$ $(1,-5)$ 或 $(-5,7)$
已知平面 $\alpha$, 直线 $l, m$, 若 $m \subset \alpha$, 则 “ $l / / m$ ” 是 “ $l / / \alpha$ ” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
如图, 边长为 2 的正方形 $A B C D$ 中, 点 $E, F$ 分别是边 $A B, B C$ 的中 点, 将 $\triangle A E D, \triangle E B F, \triangle F C D$ 分别沿 $D E, E F, F D$ 折起, 使 $A, B, C$ 三点重合于点 $A^{\prime}$, 若四面体 $A^{\prime} E F D$ 的四个顶点在同一个球面上, 则 该球的半径为

$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\frac{\sqrt{6}}{2}$
$\text{C.}$ $\frac{\sqrt{11}}{2}$
$\text{D.}$ $\frac{\sqrt{5}}{2}$
设 $a=\sin 7$, 则
$\text{A.}$ $a^2 < 2^a < \log _2|a|$
$\text{B.}$ $\log _2|a| < 2^a < a^2$
$\text{C.}$ $a^2 < \log _2|a| < 2^a$
$\text{D.}$ $\log _2|a| < a^2 < 2^a$
将函数 $f(x)=A \cos (\omega x+\varphi)(A>0, \omega>0,-\pi < \varphi < 0)$ 的图象上所有点 向右平移 $\frac{\pi}{6}$ 个单位长度, 得到如图所示的函数 $y=g(x)$ 的图象, 则 $f(0)+f\left(\frac{\pi}{3}\right)=$
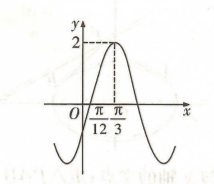
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ -1
已知: $A(-2,0), B(2,0), C(0,2), E(-1,0), F(1,0)$, 一束光线从 $F$ 点 出发射到 $B C$ 上的 $D$ 点经 $B C$ 反射后, 再经 $A C$ 反射, 落到线段 $A E$ 上 (不含端点). 则 $F D$ 斜率的取值范围是
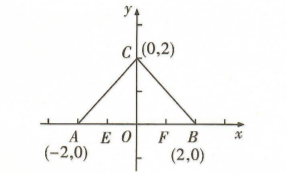
$\text{A.}$ $(-\infty,-2)$
$\text{B.}$ $(0,+\infty)$
$\text{C.}$ $(1,+\infty)$
$\text{D.}$ $(4,+\infty)$
多选题 (共 4 题 ),每题有多个选项正确
已知 $a, b, c$ 为非零实数, 且 $a-b \geqslant 0$, 则下列结论正确的有
$\text{A.}$ $a+c \geqslant b+c$
$\text{B.}$ $-a \leqslant-b$
$\text{C.}$ $a^2 \geqslant b^2$
$\text{D.}$ $\frac{1}{a b^2} \geqslant \frac{1}{b a^2}$
设 $\omega>0$, 函数 $f(x)=-\sqrt{3} \sin \omega x+\cos \omega x$ 在区间 $\left(0, \frac{\pi}{2}\right]$ 上有零点, 则 $\omega$ 的值可以是
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{5}{6}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{2}{3}$
如图, $P_1$ 是一块半径为 1 的圆形纸板, 在 $P_1$ 的左下端剪去一个半径为 $\frac{1}{2}$ 的半圆后得到图形 $P_2$, 然后依次剪去一个更小的半圆 (其直径为前 一个前掉半圆的半径) 得图形 $P_3, P_4, \cdots, P_n, \cdots$, 记纸板 $P_n$ 的周长为 $L_n$, 面积为 $S_n$, 则下列说法正确的是
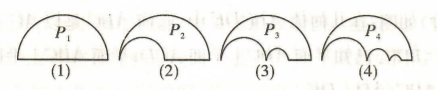
$\text{A.}$ $L_3=\frac{7}{4} \pi+\frac{1}{2}$
$\text{B.}$ $S_3=\frac{11}{32} \pi$
$\text{C.}$ $L_n=\pi\left[2-\left(\frac{1}{2}\right)^{n-1}\right]+\left(\frac{1}{2}\right)^{n+1}$
$\text{D.}$ $S_{n+1}=S_n-\frac{\pi}{2^{2 n+1}}$
已知 $a>b, c>d, \frac{\mathrm{e}^a}{a+1}=\frac{\mathrm{e}^b}{b+1}=1.01,(1-c) \mathrm{e}^c=(1-d) \mathrm{e}^d=0.99$, 则
$\text{A.}$ $a+b>0$
$\text{B.}$ $c+d>0$
$\text{C.}$ $a+d>0$
$\text{D.}$ $b+c>0$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知 $\mathrm{i}$ 是虚数单位, 如图, 在复平面内, 点 $A$ 对应的复数为 $z_1$, 若 $\frac{z_2}{z_1}=$ $\mathrm{i}$, 则 $z_2=$
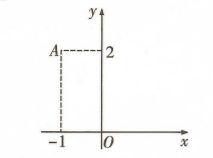
已知等边三角形 $A B C$ 的边长为 6 , 点 $P$ 满足 $3 \overrightarrow{P A}+2 \overrightarrow{P B}+\overrightarrow{P C}=\mathbf{0}$, 则 $|\overrightarrow{P A}|=$
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n$, 对任意 $n \in \mathbf{N}^*, S_n=(-1)^n a_n+\frac{1}{2^n}+n-3$ 且 $\left(a_{n+1}-p\right)\left(a_n-p\right) < 0$ 恒成立, 则实数 $p$ 的取值范围是
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图, 多面体 $A B C D E F$ 中, 底面 $A B C D$ 为正方形, $D E \perp$ 平面 $A B C D$, $C F / / D E$, 且 $A B=D E=2, C F=1, G$ 为棱 $B C$ 的中点, $H$ 为棱 $D E$ 上的 动点, 有下列结论:
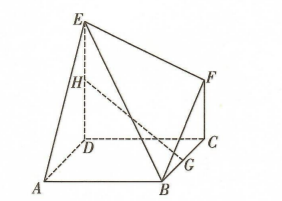
(1) 当 $H$ 为 $D E$ 的中点时, $G H / /$ 平面 $A B E$;
(2) 存在点 $H$, 使得 $G H \perp A E$;
(3)三棱雉 $B-G H F$ 的体积为定值;
(4) 三棱雉 $E-B C F$ 的外接球的表面积为 $14 \pi$.
其中正确的结论序号为 ( ) (填写所有正确结论的序号)
已知等差数列 $\left\{a_n\right\}$ 前三项的和为 $-9$, 前三项的积为 $-15$.
(1) 求等差数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $\left\{a_n\right\}$ 为递增数列, 求数列 $\left\{\left|a_n\right|\right\}$ 的前 $n$ 项和 $S_n$.
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 其外接圆的半 径为 $\sqrt{3}$, 且满足 $4 \sqrt{3} \sin B \cos C=2 a-c$.
(1)求角 $B$;
(2) 若 $A C$ 边上的中线长为 $\frac{5}{2}$, 求 $\triangle A B C$ 的面积.
2022 年 9 月 28 日晩, 中国女排在世锦赛小组赛第三轮比赛中, 又一次以 $3: 0$ 的比分酣畅淋漓地战胜了老对手日本女排, 冲上了热搜 榜第八位, 令国人振奋! 同学们, 你们知道排球比赛的规则和积分制 吗? 其规则是: 每场比赛采用 “ 5 局 3 胜制” (即有一支球队先胜 3 局即 获胜, 比赛结束). 比赛排名采用积分制, 积分规则如下: 比赛中, 以 3 : 0 或 $3: 1$ 取胜的球队积 3 分, 负队积 0 分; 以 $3: 2$ 取胜的球队积 2 分, 负队积 1 分. 已知甲、乙两队比赛, 甲队每局获胜的概率为 $\frac{2}{3}$.
(1) 如果甲、乙两队比赛 1 场, 求甲队的积分 $X$ 的概率分布列和数学 期望;
(2)如果甲、乙两队约定比赛 2 场, 求两队积分相等的概率.
如图, 在几何体 $A B C D E$ 中, 底面 $A B C$ 是以 $A C$ 为斜边的等腰 直角三角形. 已知平面 $A B C \perp$ 平面 $A C D$, 平面 $A B C \perp$ 平面 $B C E, D E / /$ 平面 $A B C, A D \perp D E$.
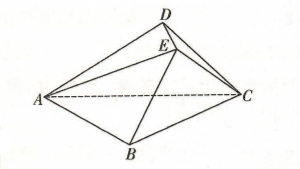
(1)证明: $D E \perp$ 平面 $A C D$;
(2)若 $A C=2 C D=2$, 设 $M$ 为棱 $B E$ 的中点, 求当几何体 $A B C D E$ 的体 积取最大值时 $A M$ 与 $C D$ 所成角的正切值.
如图所示, 已知椭圆 $C: \frac{x^2}{6}+\frac{y^2}{3}=1$ 与直线 $l: \frac{x}{6}+\frac{y}{3}=1$. 点 $P$ 在 直线 $l$ 上, 由点 $P$ 引椭圆 $C$ 的两条切线 $P A, P B$, 点 $A, B$ 为切点, $O$ 是 坐标原点.
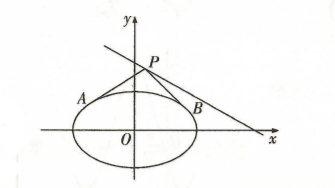
(1) 若点 $P$ 为直线 $l$ 与 $y$ 轴的交点,求 $\triangle P A B$ 的面积 $S$;
(2)若 $O D \perp A B, D$ 为垂足, 求证: 存在定点 $Q$, 使得 $|D Q|$ 为定值.
已知函数 $f(x)=x \mathrm{e}^{n x}-n x\left(n \in \mathbf{N}^*\right.$ 且 $\left.n \geqslant 2\right)$ 的图象与 $x$ 轴交于 $P, Q$ 两点, 且点 $P$ 在点 $Q$ 的左侧.
(1) 求点 $P$ 处的切线方程 $y=g(x)$, 并证明: $x \geqslant 0$ 时, $f(x) \geqslant g(x)$.
(2) 若关于 $x$ 的方程 $f(x)=t$ ( $t$ 为实数) 有两个正实根 $x_1, x_2$, 证明: $\left|x_1-x_2\right| < \frac{2 t}{n \ln n}+\frac{\ln n}{n}$.