如图所示, 已知椭圆 $C: \frac{x^2}{6}+\frac{y^2}{3}=1$ 与直线 $l: \frac{x}{6}+\frac{y}{3}=1$. 点 $P$ 在 直线 $l$ 上, 由点 $P$ 引椭圆 $C$ 的两条切线 $P A, P B$, 点 $A, B$ 为切点, $O$ 是 坐标原点.
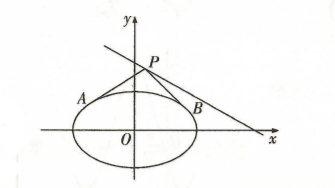
(1) 若点 $P$ 为直线 $l$ 与 $y$ 轴的交点,求 $\triangle P A B$ 的面积 $S$;
(2)若 $O D \perp A B, D$ 为垂足, 求证: 存在定点 $Q$, 使得 $|D Q|$ 为定值.

(1) 若点 $P$ 为直线 $l$ 与 $y$ 轴的交点,求 $\triangle P A B$ 的面积 $S$;
(2)若 $O D \perp A B, D$ 为垂足, 求证: 存在定点 $Q$, 使得 $|D Q|$ 为定值.