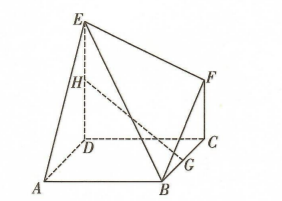
如图, 多面体 $A B C D E F$ 中, 底面 $A B C D$ 为正方形, $D E \perp$ 平面 $A B C D$, $C F / / D E$, 且 $A B=D E=2, C F=1, G$ 为棱 $B C$ 的中点, $H$ 为棱 $D E$ 上的 动点, 有下列结论:

(1) 当 $H$ 为 $D E$ 的中点时, $G H / /$ 平面 $A B E$;
(2) 存在点 $H$, 使得 $G H \perp A E$;
(3)三棱雉 $B-G H F$ 的体积为定值;
(4) 三棱雉 $E-B C F$ 的外接球的表面积为 $14 \pi$.
其中正确的结论序号为 （　　） (填写所有正确结论的序号)