科数网

如图,

P_{1}

是一块半径为 1 的圆形纸板, 在

P_{1}

的左下端剪去一个半径为

\frac{1}{2}

的半圆后得到图形

P_{2}

, 然后依次剪去一个更小的半圆 (其直径为前一个前掉半圆的半径) 得图形

P_{3}, P_{4}, \dots, P_{n}, \dots

, 记纸板

P_{n}

的周长为

L_{n}

, 面积为

S_{n}

, 则下列说法正确的是

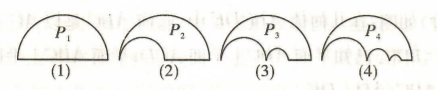
A.

L_{3} = \frac{7}{4} π + \frac{1}{2}

B.

S_{3} = \frac{11}{32} π

C.

L_{n} = π [2 - {(\frac{1}{2})}^{n - 1}] + {(\frac{1}{2})}^{n + 1}

D.

S_{n + 1} = S_{n} - \frac{π}{2^{2 n + 1}}

0 人点赞 135 次查看白板加入试卷

答案与解析：

答案仅限会员可见微信内自动登录或手机登录或微信扫码注册登录点击我要开通VIP