如图, 在几何体 $A B C D E$ 中, 底面 $A B C$ 是以 $A C$ 为斜边的等腰 直角三角形. 已知平面 $A B C \perp$ 平面 $A C D$, 平面 $A B C \perp$ 平面 $B C E, D E / /$ 平面 $A B C, A D \perp D E$.


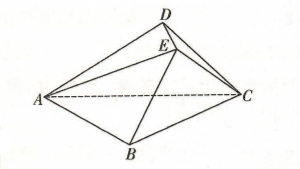
(1)证明: $D E \perp$ 平面 $A C D$;
(2)若 $A C=2 C D=2$, 设 $M$ 为棱 $B E$ 的中点, 求当几何体 $A B C D E$ 的体 积取最大值时 $A M$ 与 $C D$ 所成角的正切值.