一、单选题 (共 9 题 ),每题只有一个选项正确
1. 设 , 其中符号函数 区域 , 则
2. 设有向曲线 上任一点 处的切向量为 , 则将 曲线积分 化为第一类曲线积分的结果为
;
;
;
.
3. 若曲线积分 的结果与路径无关, 则 .
2
4. 设 为曲面 在 平面上方的部分, 则
5. 如图, 正方形
被其对角线划分为四个 区域
, 则
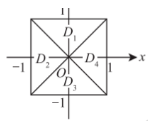
.
.
.
.
6. 设区域 由曲线 围成, 则
.
.
.
.
7. 设函数 连续, 区域 , 则 等于
.
.
.
8. 是闭区域 , 则
9. 设 , 其中积分曲面 , 取外侧, 则
0
.
.
.
二、填空题 (共 12 题 ),请把答案直接填写在答题纸上
10. 设 是直线 上点 到点 的一段弧, 则
11.
(其中 是 上从点 到点 的一段弧 .
12. 曲线 在点 处的切线方程是
13. 设闭区域 由光滑曲线 围成, 的面积等于 是 的取正向的 边界曲线, 则
14. 曲线 在点 处的曲率圆方程为
15. 曲线 的弧长为
16. 经过 和 且平行于 轴的平面方程为
17. 设 是球面 的外侧, 是其外法向量的方向余弦,则
18. 设函数 可微, 在点 处指向点 的方向导数等于 ,指向点 的方向导数等于 , 则 在点 处的最大方向导数为
19. 设函数 在曲面 上连续, 则曲面积分
20. 设 ,曲面 与曲面 相切,则
21. 设 , 则函数在 处的全微分为
三、解答题 (共 19 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
22. 计算第二型曲面积分
其中 是圆柱面 和平面 所围成的立 体的表面外侧.
23. 设空间曲线 为圆周 上从点 经过点 , 到点 的有向曲线段. (1) 若 , ) 为 上的连续函数, 将 转化为对弧长的曲线积分; (2) 利用 (1) 中 的结论, 计算 .
24. 设函数 在 ) 内可导, 满足关系式 , 且 , 求曲线 的渐近线.
25. 计算 , 其中 为圆周 , 逆时针方向.
26. 计算曲线积分 , 其中
27. 求曲线积分: ,其中
28. 求曲面积分: ,其中 由 ,柱面 以及三个坐标面在第一卦 限所围曲面外侧.
29. 计算积分 。 解: 极坐标: 令 , 则
30. 已知曲线积分 与路径无关, 其中 具有连续的导数, 且 , 求 .
31. 设抛物线 过原点, 当 时, , 又该抛物线与直线 及 轴 围成平面图形的面积为 , 求 使该图形绕 轴旋转一周而成的旋转体体积 最小
32. 求曲线积分 , 其中 沿 , 逆时针方向。
33. 计算 , 其中 是由 及 所围成的区域。
34. 设函数 和 有连续导数, 且 为平面上任意简 单光滑闭曲线, 取逆时针方向, 围成的平面区域为 , 已知
求 和 。
35. 设 一阶连续可导,
曲面 为抛物面 被平面 所截的下面部分 的内侧, 为 的正向边界,求
36. 设空间曲线 从 轴正向往负向看为逆时针方向, 计算曲线积分
37. 多元设平面区域为 , 若表达式为
且 , 试求 .
38. 求曲线 在 上的弧长.
39. 计算三重积分 ,其 中 是由曲面 围成的区域在第一卦 限部分.
40. 已知曲线型构件 的线密度为 , 求 的质量.