单选题 (共 6 题 ),每题只有一个选项正确
《义务教育课程标准 (2022 年版)》首次把学生学会炒菜纳入劳动教育课程, 并做出 明确规定. 某班有 7 名学生已经学会炒的菜品的种数依次为: $3,5,4,6,3,3,4$. 则 这组数据的众数和中位数分别是( )
$\text{A.}$ 3,4
$\text{B.}$ 4,3
$\text{C.}$ 3,3
$\text{D.}$ 4,4
已知拋物线 $v=x^{2}+m x$ 的对称轴为直线 $x=2$, 则关于 $x$ 的方程 $x^{2}+m x=5$ 的根是 ( )
$\text{A.}$ $0,4$
$\text{B.}$ $1,5$
$\text{C.}$ $1,-5$
$\text{D.}$ $-1,5$
已知 $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right)$ 为直线 $y=-2 x+3$ 上的三个点, 且 $x_{1} < x_{2} < x_{3}$, 则以下判断正确的是 ( )
$\text{A.}$ 若 $x_{1} x_{2}>0$, 则 $y_{1} y_{3}>0$
$\text{B.}$ 若 $x_{1} x_{3} < 0$, 则 $y_{1} y_{2}>0$
$\text{C.}$ 若 $x_{2} x_{3}>0$, 则 $y_{1} y_{3}>0$
$\text{D.}$ 若 $x_{2} x_{3} < 0$, 则 $y_{1} y_{2}>0$
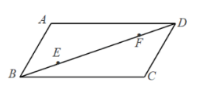
如图, 在平行四边形 $A B C D$ 中, $A D=2 A B=2, \angle A B C=60^{\circ}, E, F$ 是对角线 $B D$ 上的动点, 且 $B E=D F, M, N$ 分别是边 $A D$, 边 $B C$ 上的动点. 下列四种说法:
(1)存在无数个平行四边形 MENF;
(2)存在无数个矩形 $M E N F$;
(3)存在无数个菱形 $M E N F$ ;
(4)存在无数个正方形 MENF.
其中正确的个数是()
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知点 $P(a, b)$ 在直线 $y=-3 x-4$ 上, 且 $2 a-5 b \leqslant 0$, 则下列不等式一定成立的是 ( )
$\text{A.}$ $\frac{a}{b} \leqslant \frac{5}{2}$
$\text{B.}$ $\frac{a}{b} \geqslant \frac{5}{2}$
$\text{C.}$ $\frac{b}{a} \geqslant \frac{2}{5}$
$\text{D.}$ $\frac{b}{a} \leqslant \frac{2}{5}$
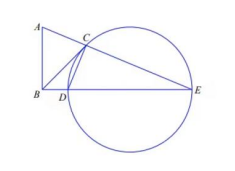
已知三角形 $\mathrm{ABE}$ 为直角三角形, $\angle \mathrm{ABE}=90^{\circ}, \mathrm{BC}$ 为圆 $\mathrm{O}$ 切线, $\mathrm{C}$ 为切点, $\mathrm{CA}=\mathrm{CD}$, 则 $\triangle \mathrm{ABC}$ 和 $\triangle$ $\mathrm{CDE}$ 面积之比为()
$\text{A.}$ $1: 3$
$\text{B.}$ $1: 2$
$\text{C.}$ $\sqrt{2}: 2$
$\text{D.}$ $1: 5$