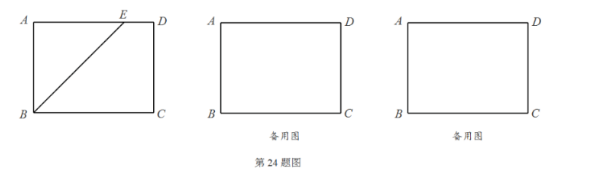
如图, 在矩形 $A B C D$ 中, $A B=6, B C=8$, 动点 $E$ 从点 $A$ 出发, 沿边 $A D, D C$ 向点 $C$ 运动, $A, D$ 关于直线 $B E$ 的对称点分别为 $M, N$, 连结 $M N$.
(1) 如图, 当 $E$ 在边 $A D$ 上且 $D E=2$ 时, 求 $\angle A E M$ 的度数.
(2) 当 $N$ 在 $B C$ 延长线上时, 求 $D E$ 的长, 并判断直线 $M N$ 与直线 $B D$ 的位置关系, 说明理由.
(3) 当直线 $M N$ 恰好经过点 $C$ 时, 求 $D E$ 的长.