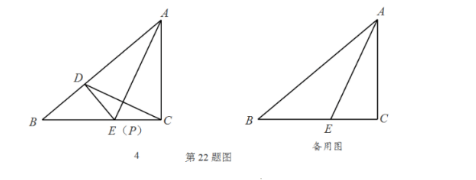
如图, 在 $\triangle A B C$ 中, $\angle A B C=40^{\circ}, \angle A C B=90^{\circ}, A E$ 平分 $\angle B A C$ 交 $B C$ 于点 $E . P$ 是边 $B C$ 上的动点(不与 $B$, $C$ 重合), 连结 $A P$, 将 $\triangle A P C$ 沿 $A P$ 翻折得 $\triangle A P D$, 连结 $D C$, 记 $\angle B C D=\alpha$.
(1) 如图, 当 $P$ 与 $E$ 重合时, 求 $\alpha$ 的度数.
(2) 当 $P$ 与 $E$ 不重合时, 记 $\angle B A D=\beta$, 探究 $\alpha$ 与 $\beta$ 的数量关系.
(1) 如图, 当 $P$ 与 $E$ 重合时, 求 $\alpha$ 的度数.
(2) 当 $P$ 与 $E$ 不重合时, 记 $\angle B A D=\beta$, 探究 $\alpha$ 与 $\beta$ 的数量关系.
