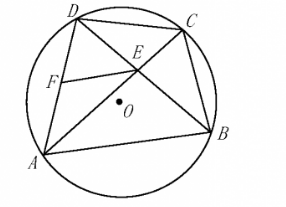
如图, 四边形 $\mathrm{ABCD}$ 内接于 $\odot 0$, 对角线 $\mathrm{AC}, \mathrm{BD}$ 相交于点 $\mathrm{E}$, 点 $\mathrm{F}$ 在边 $\mathrm{AD}$ 上, 连 接 EF.
(1) 求证: $\triangle \mathrm{ABE} \sim \triangle \mathrm{DCE}$;
(2) 当 $\widehat{\mathrm{DC}}=\widehat{\mathrm{CB}}, \angle \mathrm{DFE}=2 \angle \mathrm{CDB}$ 时, 则 $\frac{\mathrm{AE}}{\mathrm{BE}}-\frac{\mathrm{DE}}{\mathrm{CE}}= ; \frac{\mathrm{AF}}{\mathrm{AB}}+\frac{\mathrm{FE}}{\mathrm{AD}}=$; $\frac{1}{\mathrm{AB}}+\frac{1}{\mathrm{AD}}-\frac{1}{\mathrm{AF}}=$ (直接将结果填写在相应的横线上)
(3) (1)记四边形 $\mathrm{ABCD}, \triangle \mathrm{ABE}, \triangle \mathrm{CDE}$ 的面积依次为 $\mathrm{S}, \mathrm{S}_{1}, \mathrm{~S}_{2}$, 若满足 $\sqrt{\mathrm{S}}=\sqrt{\mathrm{S}_{1}}+\sqrt{\mathrm{S}_{2}}$,
试判断 $\triangle A B E, \triangle C D E$ 的形状, 并说明理由.
(2)当 $\widehat{D C}=\widehat{C B}, A B=m, A D=n, C D=p$ 时, 试用含 $m, n, p$ 的式子表示 $A E \cdot C E$.
(1) 求证: $\triangle \mathrm{ABE} \sim \triangle \mathrm{DCE}$;
(2) 当 $\widehat{\mathrm{DC}}=\widehat{\mathrm{CB}}, \angle \mathrm{DFE}=2 \angle \mathrm{CDB}$ 时, 则 $\frac{\mathrm{AE}}{\mathrm{BE}}-\frac{\mathrm{DE}}{\mathrm{CE}}= ; \frac{\mathrm{AF}}{\mathrm{AB}}+\frac{\mathrm{FE}}{\mathrm{AD}}=$; $\frac{1}{\mathrm{AB}}+\frac{1}{\mathrm{AD}}-\frac{1}{\mathrm{AF}}=$ (直接将结果填写在相应的横线上)
(3) (1)记四边形 $\mathrm{ABCD}, \triangle \mathrm{ABE}, \triangle \mathrm{CDE}$ 的面积依次为 $\mathrm{S}, \mathrm{S}_{1}, \mathrm{~S}_{2}$, 若满足 $\sqrt{\mathrm{S}}=\sqrt{\mathrm{S}_{1}}+\sqrt{\mathrm{S}_{2}}$,
试判断 $\triangle A B E, \triangle C D E$ 的形状, 并说明理由.
(2)当 $\widehat{D C}=\widehat{C B}, A B=m, A D=n, C D=p$ 时, 试用含 $m, n, p$ 的式子表示 $A E \cdot C E$.
