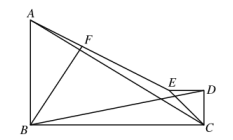
已知 $\triangle \mathrm{ABC}$ 是直角三角形, $\angle \mathrm{B}=90^{\circ}, \mathrm{AB}=3, \mathrm{BC}=5, \mathrm{AE}=2 \sqrt{5}$, 连接 $\mathrm{CE}$ 以 $\mathrm{CE}$ 为底作直角三角形 $\mathrm{CDE}$ 且 $\mathrm{CD}=\mathrm{DE}$ 。 $\mathrm{F}$ 是 $\mathrm{AE}$ 边上的一点, 连接 $\mathrm{BD}$ 和 $\mathrm{BF}, \mathrm{BD}$ 且 $\angle \mathrm{FBD}=45^{\circ}$, 则 $\mathrm{AF}$ 长为