单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\{-1,0,1,2\}, B=\left\{y \mid y=2^x\right\}$, 则 $A \cap B$ 表示的集合为
$\text{A.}$ $\{-1\}$
$\text{B.}$ $\{-1,0\}$
$\text{C.}$ $\{1,2\}$
$\text{D.}$ $\{0,1,2\}$
复数 $z=\frac{3-\mathrm{i}}{1+\mathrm{i}}-1$, 则 $|z|=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $2$
$\text{D.}$ $5$
某医疗公司引进新技术设备后, 销售收入(包含医疗产品收入和其他收入) 逐年翻一番,据 统计该公司销售收入情况如图 1 所示, 则下列说 法错误的是
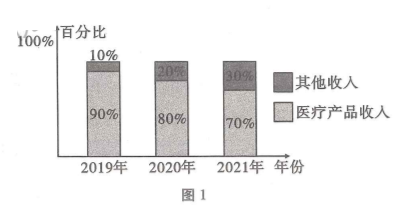
$\text{A.}$ 该地区 2021 年的销售收入是 2019 年的 4 倍
$\text{B.}$ 该地区 2021 年的医疗产品收入比 2019 年和 2020 年的医疗产品收入总和还要多
$\text{C.}$ 该地区 2021 年其他收入是 2020 年的其他收入的 3 倍
$\text{D.}$ 该地区 2021 年的其他收入是 2019 年的其他收入的 6 倍
我国古代数学名著《九章算术》对立体几何有深人的研究, 从其中一些数 学用语可见, 譬如 “阳马” 意指底面为矩形, 一侧棱垂直于底面的四棱 锥. 某 “阳马” 的三视图如图 2 所示, 则它的最长侧棱与底面所成角的正 切值为
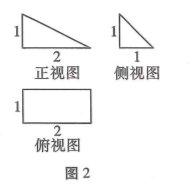
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $1$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{6}}{6}$
已知焦点在坐标轴上且中心在原点的双曲线的一条渐近线方程为 $2 y=x$, 若该双曲线过点 $(1,1)$, 则它的方程为
$\text{A.}$ $4 y^2-x^2=3$
$\text{B.}$ $4 x^2-y^2=3$
$\text{C.}$ $2 y^2-x^2=1$
$\text{D.}$ $2 x^2-y^2=1$
已知直线 $(m+2) x+(m-1) y-2 m-1=0(m \in \mathbf{R})$ 与圆 $C: x^2-4 x+y^2=0$, 则下列说法错误的是
$\text{A.}$ 对 $\forall m \in \mathbf{R}$, 直线恒过一定点
$\text{B.}$ $\exists m \in \mathbf{R}$, 使直线与圆相切
$\text{C.}$ 对 $\forall m \in \mathbf{R}$, 直线与圆一定相交
$\text{D.}$ 直线与圆相交且直线被圆所截得的最短弦长为 $2 \sqrt{2}$
以下关于 $f(x)=\sin x \cos x-\cos ^2 x+\frac{1}{2}$ 的命题, 正确的是
$\text{A.}$ 函数 $f(x)$ 在区间 $\left(0, \frac{2 \pi}{3}\right)$ 上单调递增
$\text{B.}$ 直线 $x=\frac{\pi}{8}$ 是函数 $y=f(x)$ 图象的一条对称轴
$\text{C.}$ 点 $\left(\frac{\pi}{4}, 0\right)$ 是函数 $y=f(x)$ 图象的一个对称中心
$\text{D.}$ 将函数 $y=f(x)$ 图象向左平移 $\frac{\pi}{8}$ 个单位, 可得到 $y=\frac{\sqrt{2}}{2} \sin 2 x$ 的图象
在 $\triangle A B C$ 中, $a, b, c$ 分别为角 $A, B, C$ 的对边, 且满足 $b-a=2 b \sin ^2 \frac{C}{2}$, 则 $\triangle A B C$ 的形状为
$\text{A.}$ 直角三角形
$\text{B.}$ 等边三角形
$\text{C.}$ 直角三角形或等腰三角形
$\text{D.}$ 等腰直角三角形
小明家订了一份牛奶, 送奶人可能在早上 $6:30 \sim 7:00$ 间把牛奶送到小明家, 小明出门去 上学的时间在早上 $6:50 \sim 7:10$ 之间, 则小明有离丙家之前能得到牛奶的概率是
$\text{A.}$ $\frac{1}{12}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{7}{8}$
$\text{D.}$ $\frac{11}{12}$
已知符号函数 $\operatorname{sgn} x=\left\{\begin{array}{ll}1, x>0, & -1 \\ 0, & x=0, \\ -1, x < 0,\end{array}\right.$ 数 $f(x)$ 满足 $f(1-x)=f(1+x), f(x+2)=f(x)$, 当 $x \in[0,1]$ 时, $f(x)=\sin \left(\frac{\pi}{2} x\right)$, 则
$\text{A.}$ $\operatorname{sgn}(f(x))>0$
$\text{B.}$ $f\left(\frac{4041}{2}\right)=1$
$\text{C.}$ $\operatorname{sgn}(f(2 k))=0(k \in \mathbf{Z})$
$\text{D.}$ $\operatorname{sgn}(f(2 k))=|\operatorname{sgn} k|(k \in \mathbf{Z})$
已知直线 $l$ 与曲线 $y=\mathrm{e}^x$ 相切, 切点为 $P$, 直线 $l$ 与 $x$ 轴、 $y$ 轴分别交于点 $A, B$, $O$为坐标原点. 若 $\triangle O A B$ 的面积为 $\frac{1}{\mathrm{e}}$, 则点 $P$ 的个数是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如图 3, 已知四面体 $A B C D$ 中, $A B=A C=B D=C D=2 \sqrt{2}, A D=B C=2$, $E, F$ 分别是 $A D, B C$ 的中点. 若用一个与直线 $E F$ 垂直, 且与四面体 的每一个面都相交的平面 $\alpha$ 去截该四面体, 由此得到一个多边形截 面, 则该多边形截面面积的最大值为
$\text{A.}$ $1$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $2$
$\text{D.}$ $2 \sqrt{2}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $\boldsymbol{a}=(1,3), \boldsymbol{b}=(3,4)$, 若 $(m \boldsymbol{a}-\boldsymbol{b}) / /(\boldsymbol{a}+\boldsymbol{b})$, 则 $m=$
$\left(1+\frac{1}{x^2}\right)(1+x)^6$ 的展开式中 $x^2$ 的系数为
若 $a=\dfrac{\left(1-\log _6 3\right)^2+\log _6 2 \cdot \log _6 18}{\log _{\sqrt{6}} 2}$, 则 $a$ 的值为
抛物线 $y^2=2 p x(p>0)$ 的焦点为 $F$, 直线 $l$ 过点 $F$ 且与抛物线交于点 $M, N$ (点 $N$ 在 $x$ 轴上 方), 点 $E$ 为坐标轴上 $F$ 右侧的一点, 已知 $|N F|=|E F|=3|M F|, S_{\triangle M N E}=3 \sqrt{3}$, 若点 $N$ 在双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的一条渐近线上, 则双曲线的离心率为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
随着人民生活水平的不断提高, “衣食住行” 愈发被人们所重视, 其中对饮食的要求也愈来愈高. 某地区为了解当地餐饮情况, 随机抽取了 100 人对该地区的餐饮情况进行了问卷调查. 请根据下面尚末完成并有局部污损的频率分布表和频率分布直方图 (如图 4) 解决下列问题.
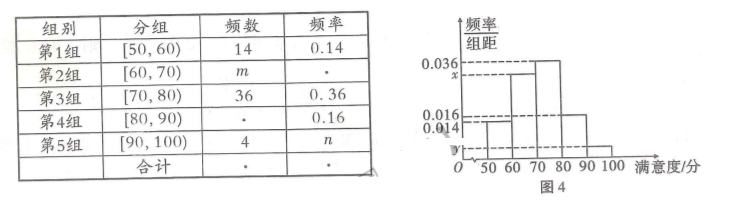
(1) 求 $m, n, x, y$ 的值;
(2) 求中位数;
(3) 若将满意度在 80 分以上的人群称为 “美食客”, 将频率视为概率, 用样本估计总体, 从该地区中随机抽取 3 人, 记其中 “美食客” 的人数为 $\xi$, 求 $\xi$ 的分布列和数学期望.
已知数列 $\left\{a_n\right\}$ 是递增的等比数列. 设其公比为 $q$, 前 $n$ 项和为 $S_n$, 并且唡足 $a_1+a_5=34,8$ 是 $a_2$ 与 $a_4$ 的等比中项.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=n \cdot a_n, T_n$ 是 $b_n$ 的前 $n$ 项和, 求使 $T_n-n \cdot 2^{n+1}>-100$ 成立的最大正整数 $n$ 的值.
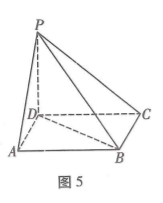
如图 5, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 是平行四边形, $P D \perp$ 平面 $A B C D, P D=A D=B D=1, A B=\sqrt{2}$.
(1) 求证: 平面 $P B D \perp$ 平面 $P B C$;
(2) 试问在线段 $P C$ 上是否存在一点 $M$, 使得二面角 $M-B D-C$ 的大小为 $60^{\circ}$, 若存在求出 $\frac{P M}{M C}$ 的值; 若不存在, 请说明理由.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0, b>0)$ 过点 $\left(1, \frac{\sqrt{6}}{2}\right)$, 且离心率为 $\frac{\sqrt{2}}{2}$.
(1) 求椭圆 $C$ 的方程;
(2) 已知直线 $l: y=m x+2$ 与椭圆交于不同的两点 $P, Q$, 那么在 $x$ 轴上是否存在点 $M$, 使 $M P=M Q$ 且 $M P \perp M Q$, 若存在, 求出该直线的方程; 若不存在, 请说明理由.
已知 $f(x)=\ln x-a x+1(a \in \mathbf{R})$.
(1) 讨论 $f(x)$ 的单调性;
(2) 若 $f(x) \leqslant \frac{1}{2} a x^2-x$ 对 $x \in(0,+\infty)$ 恒成立, 求整数 $a$ 的最小值.
在平面直角坐标系 $x O y$ 中, 曲线 $C$ 的参数方程为 $\left\{\begin{array}{l}x=\sqrt{3}(\sin \theta-\cos \theta), \\ y=\sqrt{2}(\sin \theta+\cos \theta),\end{array}\right.$ 点 $O$ 为极点, $x$ 轴正半轴为极轴建立极坐标系, 直线 $l$ 的极坐标方程为 $\rho \cos \left(\theta+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}$.
(1) 求直线 $l$ 和曲线 $C$ 的直角坐标方程;
(2) 从原点 $O$ 引一条射线分别交曲线 $C$ 和直线 $l$ 于 $M, N$ 两点, 求 $\frac{12}{|O M|^2}+\frac{1}{|O N|^2}$ 的最 大值.
已知函数 $f(x)=|x+a|+\left|x-\frac{a}{2}\right|$.
(1) 当 $a=2$ 时, 求不等式 $f(x) \leqslant 5$ 的解集;
(2) 设 $a>0, b>0$ 且 $f(x)$ 的最小值为 $m$, 若 $m+\frac{3}{2} b=3$, 求 $\frac{3}{a}+\frac{2}{b}$ 的最小值.