随着人民生活水平的不断提高, “衣食住行” 愈发被人们所重视, 其中对饮食的要求也愈来愈高. 某地区为了解当地餐饮情况, 随机抽取了 100 人对该地区的餐饮情况进行了问卷调查. 请根据下面尚末完成并有局部污损的频率分布表和频率分布直方图 (如图 4) 解决下列问题.

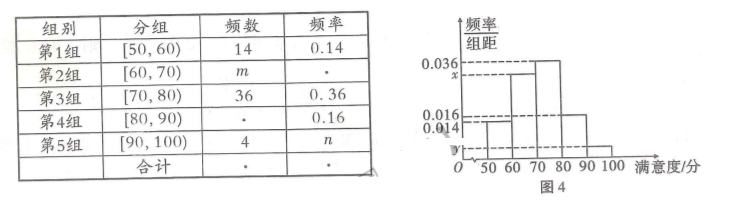
(1) 求 $m, n, x, y$ 的值;
(2) 求中位数;
(3) 若将满意度在 80 分以上的人群称为 “美食客”, 将频率视为概率, 用样本估计总体, 从该地区中随机抽取 3 人, 记其中 “美食客” 的人数为 $\xi$, 求 $\xi$ 的分布列和数学期望.