广西柳州市高级中学南宁第三中学2022高三联考（文科数学）

导出试卷

广西柳州市高级中学南宁第三中学2022高三联考（文科数学）

一、单选题（共 12 题），每题只有一个选项正确

1. 已知集合

A = {x | | x ∣< 2}, B = {- 1, 0, 2}

, 则

A \cap B =

A.

{0, 2}

B.

{- 1, 0, 2}

C.

{- 1, 0}

D.

{- 1, 2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 复数

z = \frac{2 - i}{i}

在复平面内对应的点的坐标为

A.

(1, 2)

B.

(- 1, - 2)

C.

(2, 1)

D.

(- 2, - 1)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 北京 2022 年冬奥会期间, 某大学派出了 1000 名志愿者, 为了解志愿者的工作情况, 该大学学生会将这 1000 名志原者随机编号为

1, 2, \dots, 1000

, 再从中利用系统抽样的方法抽取一个容量为 200 的样本进行问卷调査, 若所抽中的最小编号为 3 , 则所抽中的最大编号为

A.

968

B.

978

C.

988

D.

998

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 在普通高中新课程改革中, 某地实施 “

3 + 1 + 2

” 选课方案. 该方案中“2” 指的是从政治、地理、化学、生物 4 门学科中任选 2 门, 假设每门学科被述中的可能性相等, 那么政治和地理至少有一门被选中的概率是

A.

\frac{5}{6}

B.

\frac{1}{2}

C.

\frac{2}{3}

D.

\frac{1}{6}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 已知函数

f (x) = a x^{3} + b x + 2 (a \neq 0)

满足

f (- 3) = 5

, 则

f (3)

等于

A.

2

B.

- 5

C.

- 1

D.

- 3

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 已知

\frac{- \cos α + 2 \sin α}{\cos α - \sin α} = - 3

, 则

\sin 2 a =

A.

\frac{4}{5}

B.

- \frac{4}{5}

C.

1

D.

\frac{3}{5}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 设

x, y

满足约束条件

{\begin{cases} 2 x + y - 6 ⩽ 0, \\ x + y - 3 ⩾ 0, 则 z = x - 3 y 的最大值为 \\ y ⩽ 3 \end{cases}

A.

B.

- \frac{15}{2}

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 若圆锥的轴截面为等边三角形, 且面积为

2 \sqrt{3}

, 则圆锥的体积为

A.

4 \sqrt{3} π

B.

\frac{2 \sqrt{6}}{3} π

C.

\frac{8 \sqrt{3} π}{3}

D.

8 \sqrt{3} π

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 圆

(x - 1)^{2} + y^{2} = 4

截直线

l : y = k (x - 2) + 1

所得的弦长最短为

A.

\frac{\sqrt{2}}{2}

B.

C.

\sqrt{2}

D.

2 \sqrt{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 已知椭圆和双曲线有共同的焦点

F_{1}, F_{2}, P

是它们的一个交点, 且

∠ F_{1} P F_{2} = \frac{π}{3}

, 记椭圆和双曲线的离心率分别为

e_{1}, e_{2}

, 则

e_{1} \cdot e_{2}

的最小值为

A.

\frac{\sqrt{3}}{2}

B.

\frac{3}{4}

C.

\sqrt{3}

D.

3

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知数列

{a_{n}}

满足:

a_{1} = 3

, 当

n ⩾ 2

时,

a_{n} = {(\sqrt{a_{n - 1} + 1} + 1)}^{2} - 1

, 则数列

{a_{n}}

的通项公式是

A.

a_{n} = 2 n + 1

B.

a_{n} = n^{2} + 2 n

C.

a_{n} = n^{2} + 2

D.

a_{n} = 2 n^{2} + 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 已知

a = e - 1, b = 2 - \ln 2, c = e^{e} - e^{2} + 1

, 则

A.

c > b > a

B.

a > b > c

C.

a > c > b

D.

c > a > b

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 11 题），请把答案直接填写在答题纸上

13. 已知

| a | = \sqrt{3}, | b | = 2 \sqrt{3}, a \cdot b = 3

, 则

a

与

b

的夹角是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 已知函数

f (x) = (a x + b) e^{x}

, 若曲线

y = f (x)

在点

(0, f (0))

处的切线方程为

3 x - y + 1 = 0

, 则

f (1)

的值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 设

φ > 0

, 函数

f (x) = \sin (2 x + φ) - \sqrt{3} \cos (2 x + φ)

为偶函数, 则

φ

的最小值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 已知数列

{a_{n}}

的各项互异, 且

a_{n} > 0, \frac{1}{a_{n + 1}} - \frac{1}{a_{n}} = 2 (n \in N^{*})

, 则

\frac{a_{1} - a_{n}}{a_{1} a_{2} + a_{2} a_{3} + \dots + a_{n - 1} a_{n}}

=

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 某大型房地产公司对该公司 140 名一线销售员工每月进行一次目标考核, 对该月内签单总数达到 10 单及以上的员工投予该月 “金牌销售” 称号, 其余员工称为“普通销售”, 下表是该房地产公司 140 名员工 2022 年 1 月至 5 月获得“金牌销售” 称号的统计数据：

(1) 由表中看出, 可用线性回归模型拟合“金牌销售” 员丁数

y

与月份

x

之间的关系, 求

y

关于

x

的回归直线方程

y = b x + a

, 并预测该房地产公司 6 月份犾得 “金牌销售” 称号的员工人数;
(2) 为了进一步了解员工们的销售情况, 选取了员工们在 3 月份的销售数据进行分析, 统计结果如下:

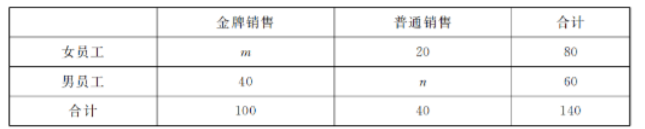
请补充上表中的数据 (直接写出

m, n

的值), 并根据上表判断是否有

95 %

的把握认为获得“金牌销售” 称号与性别有关?
参考数据

\begin{aligned} K^{2} = & \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)} \\ (其中 n = a + b + c + d) . \end{aligned}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 已知

△ A B C

的内角

A, B, C

的对边分别为

a, b, c

, 且满足

b \sin \frac{B + C}{2} = a \sin B

.
(1) 求

A

;
(2) 若

a = 4, △ A B C

的面积为

4 \sqrt{3}

, 求

△ A B C

的周长.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 如右图所示, 在四棱锥

P - A B C D

中, 平面

P A D ⊥

平面

A B C D, A B / / D C, △ P A D

是等边三角形, 已知

B D = 2 A D = 8, A B = 2 D C = 4 \sqrt{5}, M

是

P C

的中点.
(1) 证明: 平面

M B D ⊥

平面

P A D

;
(2) 求四棱雉

M - A B C D

的体积.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 已知点

P (\frac{2}{3}, \frac{2 \sqrt{6}}{3})

是椭圆

C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)

与抛物线

E : y^{2} = 2 p x (p > 0)

的一个公共点, 且椭圆与抛物线具有一个相同的焦点

F

. 过点

Q (4, 0)

且不垂直于

x

轴的直线

l

与椭圆相交于

A, B

两点.
(1) 求楉圆

C

及抛物线

E

的方程;
(2) 若点

B

关于

x

轴的对称点为点

H

, 证明: 直线

A H

与

x

轴交于定点.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 已知函数

f (x) = \ln x - x + 1, x \in (0, + \infty)

.
(1) 求函数

f (x)

的零点个数;
(2) 证明: 当

0 < x ⩽ \frac{3 π}{2}

时,

f (x) < \sin x

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22. 在平面直角坐标系

x O y

中, 曲线

C_{1}

的参数方程为

{\begin{cases} x = \frac{t}{2} \\ y = 3 - t \end{cases}

, (

t

为参数), 以坐标原点

O

为极点,

x

轴的正半轴为极轴建立极坐标系. 曲线

C_{2}

的极坐标方程为

4 ρ^{2} - 3 ρ^{2} \cos^{2} θ = 4

.
(1) 写出曲线

C_{1}

的普通方程和曲线

C_{2}

的直角坐标方程;
(2) 已知点

P

是曲线

C_{2}

上的动点. 求点

P

到曲线

C_{1}

距离的最大值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 已知函数

f (x) = | x - 1 | + | x - a |

(1) 若函数

f (x)

的值域为

[2, + \infty)

, 求实数

a

的值;
(2) 若

f (2 - a) ⩾ f (2)

, 求实数

a

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。