某大型房地产公司对该公司 140 名一线销售员工每月进行一次目标考核, 对该月内签单总数达 到 10 单及以上的员工投予该月 “金牌销售” 称号, 其余员工称为“普通销售”, 下表是该房地产公 司 140 名员工 2022 年 1 月至 5 月获得“金牌销售” 称号的统计数据：

(1) 由表中看出, 可用线性回归模型拟合“金牌销售” 员丁数 $y$ 与月份 $x$ 之间的关系, 求 $y$ 关于 $x$ 的 回归直线方程 $y=bx+a$, 并预测该房地产公司 6 月份犾得 “金牌销售” 称号的员工人数;
(2) 为了进一步了解员工们的销售情况, 选取了员工们在 3 月份的销售数据进行分析, 统计结果如下:

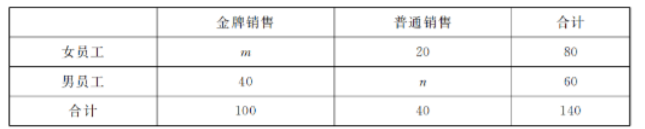
请补充上表中的数据 (直接写出 $m,n$ 的值), 并根据上表判断是否有 $95\mathrm{\%}$ 的把握认为获得“金牌 销售” 称号与性别有关?
参考数据
$$\begin{array}{rl}{K}^2=& \frac{n(ad-bc{)}^2}{(a+b)(c+d)(a+c)(b+d)}\\ & (\text{ 其中 }n=a+b+c+d).\end{array}$$