一、单选题 (共 12 题 ),每题只有一个选项正确
1. 已知集合 , 集合 , 集合 , 则
2. 已知复数 满足 , 其中 为虚数单位, 则在复平面内 对应的点位于
第一象限
第二象限
第三象限
第四象限
3. 已知数列 均为公差不为 0 的等差数列, 且满足 , 则
2
1
3
4. 已知指数函数 的图象与直线 相切于点 , 则 的解析式可能是
5. 若 满足约束条件 则 的最大值为
6. 记 为各项均为正数的等比数列 的前 项和, , 则 ( )
1
2
7. 如图是某个函数
的图象的一部分, 则该函数可能是

8. 《天才引导的过程一一数学中的伟大定理》的作者威廉 - 邓纳姆曾写道: “如果你想要做 加法你需要 0 , 如果你想要做乘法你需要 1 , 如果你想要做微积分你需要 , 如果你想要做 几何你需要 , 如果你想要做复分析你需要 , 这是数学的梦之队, 他们都在这个方程 里.” 这里指的方程就是: , 令 , 则 , 令 , 则 , 若数列 满足 为数列 的前 项和, 则下列结论正确的个数是()
① 是等比数列
②
③
④
1个
2个
3个
4个
9. 在 中, 点 为 的中点, 与 交于点 , 且满足 , 则 的值为 ( )
10. 设 , 则
11. 已知 是定义域为 的奇函数, 若 的最小正周期为 1 , 则下列 说法一定正确的是
1 是 的一个周期
12. 在 中, 角 所对的边分别为 , 若 , 且 , 则
1
2
二、填空题 (共 4 题 ),请把答案直接填写在答题纸上
13. 若单位向量 满足 , 则 与 的夹角为
14. 若 的图象向右平移 个单位长度得到 的图象, 则 的值可以是 . (写出满足条件的一个值即可)
15. 已知点 是函数 图象上的点, 当 时, 的最小值为
16. 已知关于 的方程 有 4 个不等实数根, 则 的取值范围 是
三、解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
17. 已知 .
(1) 若 , 且 时, 与 的夹角为钝角, 求 的取值范 围;
(2) 若 , 函数 , 求 的最小值.
18. 已知数列 满足 为奇数时为偶数时,
若数列 为数列 的奇数项组成的数列, 为数列 的偶数项组成的数列, 求出 , 并证明: 数列 为等差数列;
(2) 求数列 的前 22 项和.
19. 已知公比的绝对值大于 1 的无穷等比数列 中的前三项恰为 , 3,8 中的三个数, 为数列 的前 项和.
(1) 求 ;
(2)设数列 的前 项和为 , 求证: .
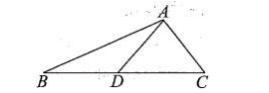
20. 如图,
中, 点
为边
上一点, 且满足
.
(1) 证明:
;
(2) 若
, 求
的面积.
21. 已知 .
(1)当 时, 恒成立, 求 的取值范围;
(2) 当 时, 求 在 上的零点个数.
22. 在直角坐标系 中, 曲线 的参数方程为 ( 为参数), 曲线 的参数方程为 为参数 .
(1) 以坐标原点为极点, 轴正半轴为极轴建立极坐标系, 求曲线 的极坐标方程与 的普通方程;
(2) 若 分别为曲线 , 曲线 上的动点, 求 的最小值.
23. 已知函数 .
(1) 若对 恒成立, 求实数 的取值范围;
(2) 若 的最小值为 4 , 且正数 满足 , 求 的最小值