单选题 (共 3 题 ),每题只有一个选项正确
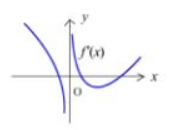
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续, 其导函数图形如图所示, 则 $f(x)$ 的极值点的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若函数 $f(x)$ 在原点连续, $F(x)=f(x)|\sin x|$, 则 $f(0)=0$ 是 $F^{\prime}(0)$ 存在的
$\text{A.}$ 充要条件
$\text{B.}$ 充分但非必要条件
$\text{C.}$ 必要但非充分条件
$\text{D.}$ 既非充分也非必要条件
设 $g(t)$ 是正值连续函数, 且 $f(x)=\int_{-a}^a|x-t| g(t) \mathrm{d} t, a>0, x \in[-a, a]$, 关于曲线 $y=f(x)$, 下列说法正确的是
$\text{A.}$ 在 $[-a, 0]$ 上是凹的, 在 $[0, a]$ 上是凸的
$\text{B.}$ 在 $[-a, 0]$ 上是凸的, 在 $[0, a]$ 上是凹的.
$\text{C.}$ 在 $[-a, a]$ 上是凹的.
$\text{D.}$ 在 $[-a, a]$ 上是凸的.