单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{x \mid-1 < x \leqslant 2\}, B=\{-2,-1,0,2,4\}$, 则 $\left(\complement_{\mathbf{R}} A\right) \cap B=$
$\text{A.}$ $\varnothing$
$\text{B.}$ $\{-1,2\}$
$\text{C.}$ $\{-2,4\}$
$\text{D.}$ $\{-2,-1,4\}$
若幕函数 $f(x)$ 的图象过点 $(4,2)$, 则 $f(2)$ 的值为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ 2
命题 “ $\forall x>1, x^{2}+1>2$ ” 的否定为
$\text{A.}$ $\exists x \leqslant 1, x^{2}+1 \leqslant 2$
$\text{B.}$ $\forall x>1, x^{2}+1 \leqslant 2$
$\text{C.}$ $\exists x>1, x^{2}+1 \leqslant 2$
$\text{D.}$ $\forall x \leqslant 1, x^{2}+1 \leqslant 2$
已知函数 $f(x)=\left\{\begin{array}{c}\left(\frac{1}{3}\right)^{x}, x \leqslant 0, \\ \log _{3} x-2, x>0,\end{array}\right.$ 则 $f(f(-3))$ 的值为
$\text{A.}$ $-3$
$\text{B.}$ $-2$
$\text{C.}$ 0
$\text{D.}$ 1
已知函数 $y=a^{x+4}+2(a>0$, 且 $a \neq 1)$ 的图象恒过点 $P$, 若角 $\alpha$ 的终边经过点 $P$, 则 $\cos \alpha$ 的值为
$\text{A.}$ $-\frac{4}{5}$
$\text{B.}$ $-\frac{2 \sqrt{2}}{3}$
$\text{C.}$ $\frac{\sqrt{2}}{3}$
$\text{D.}$ $\frac{3}{5}$
设 $m, n$ 为正数, 且 $m+n=2$, 则 $\frac{4}{m+1}+\frac{1}{n+1}$ 的最小值为
$\text{A.}$ $\frac{13}{4}$
$\text{B.}$ $\frac{9}{4}$
$\text{C.}$ $\frac{7}{4}$
$\text{D.}$ $\frac{9}{5}$
设 $a=3^{-\frac{1}{2}}, b=\log _{\frac{1}{3}} 2, c=\tan 70^{\circ}$, 则
$\text{A.}$ $a>c>b$
$\text{B.}$ $b>c>a$
$\text{C.}$ $c>b>a$
$\text{D.}$ $c>a>b$
如图的曲线就像横放的葫芦的轴截面的边缘线, 我们叫葫芦曲线(也像湖面上高低起伏 的小岛在水中的倒影与自身形成的图形, 也可以形象地称它为倒影曲线), 它对应的方程为$|y|=\left(3-\frac{1}{3}\left[\frac{3 x}{\pi}\right]\right) \cdot|\sin \omega x|(0 \leqslant x \leqslant 3 \pi)$ (其中记 $[x]$ 为不超过 $x$ 的最大整数), 且过点 $P\left(\frac{\pi}{6}, 3\right)$, 若 葫芦曲线上一点 $M$ 到 $y$ 轴的距离为 $\frac{17 \pi}{6}$, 则点 $M$ 到 $x$ 轴的距离为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
多选题 (共 4 题 ),每题有多个选项正确
使 $x-\frac{1}{x} \leqslant 0$ 成立的一个充分条件可以是
$\text{A.}$ $x < -1$
$\text{B.}$ $0 < x < 1$
$\text{C.}$ $-1 \leqslant x \leqslant 1$
$\text{D.}$ $x \leqslant 1$
关于函数 $f(x)=2 \sin \left(2 x-\frac{\pi}{3}\right)$, 下列说法中正确的是
$\text{A.}$ 其最小正周期为 $\pi$
$\text{B.}$ 其图象由 $y=2 \sin 2 x$ 向右平移 $\frac{\pi}{3}$ 个单位而得到
$\text{C.}$ 其表达式可以写成 $f(x)=2 \cos \left(2 x-\frac{5 \pi}{6}\right)$
$\text{D.}$ 其图象关于点 $\left(-\frac{\pi}{3}, 0\right)$ 对称
下列说法中正确的是
$\text{A.}$ 若 $\alpha$ 是第二象限角, 则点 $P(\cos (-\alpha), \tan (\pi+\alpha))$ 在第三象限
$\text{B.}$ 圆心角为 $1 \mathrm{rad}$, 半径为 2 的扇形面积为 2
$\text{C.}$ 利用二分法求方程 $\log _{2} x=4-x$ 的近似解,可以取的一个区间是 $(2,3)$
$\text{D.}$ 若 $\alpha \in\left(\pi, \frac{3 \pi}{2}\right)$, 且 $\sin \alpha+\cos \alpha=-\frac{7}{5}$, 则 $\sin \alpha-\cos \alpha=-\frac{1}{5}$
规定 $\max \{a, b\}=\left\{\begin{array}{ll}a, & a \geqslant b, \\ b, & a < b .\end{array}\right.$ 若函数 $f(x)=\max \{\sin x, \cos x\}$, 则
$\text{A.}$ $f(x)$ 是以 $2 \pi$ 为最小正周期的周期函数
$\text{B.}$ $f(x)$ 的值域是 $[-1,1]$
$\text{C.}$ 当且仅当 $2 k \pi+\pi < x < 2 k \pi+\frac{3 \pi}{2}(k \in \mathbf{Z})$ 时, $f(x) < 0$
$\text{D.}$ 当且仅当 $x \in\left[k \pi+\frac{\pi}{4}, k \pi+\frac{\pi}{2}\right](k \in \mathbf{Z})$ 时, 函数 $f(x)$ 单调递增 【答案】 $\mathrm{AC}$
填空题 (共 7 题 ),请把答案直接填写在答题纸上
$\mathrm{e}^{\ln 2}+27^{-\frac{1}{2}}-\tan \frac{\pi}{4}+\lg 10^{-2}=$
函数 $f(x)=\sqrt{1-x}+\ln (x+1)$ 的定义域为
若函数 $f(x)=\log _{\frac{1}{2}}\left(a x-x^{2}\right)$ 在 $(2,3)$ 单调递增, 则实数 $a$ 的取值范围是
已知函数 $f(x)=\left\{\begin{array}{cc}\left|4^{x}-1\right|, & x \leqslant 1, \\ \log _{2} x+3, & x>1,\end{array}\right.$ 集合 $M=\left\{x \mid f^{2}(x)-\left(2 t+\frac{1}{2}\right) f(x)+t=0\right\}$, 若集合$M$中有 3 个元素, 则实数 $t$ 的取值范围是
在(1) $A \cup B=B ;$ (2) “ $x \in A$ ” 是 “ $x \in B$ ” 的充分条件; (3) “ $x \in \complement_{\mathbf{R}} A$ ” 是 “ $x \in \complement_{\mathbf{R}} B$ ” 的 必要条件, 在这三个条件中任选一个, 补充到本题第(2)问的横线处, 求解下列问题.
问题: 已知集合 $A=\{x \mid a \leqslant x \leqslant a+2\}, B=\{x \mid(x+1)(x-3) < 0\}$.
(1)当 $a=2$ 时, 求 $A \cap B$;
(2) 若 ( ) , 求实数 $a$ 的取值范围.
注: 如果选择多个条件分别解答, 按第一个解答计分.
已知 $\tan (\pi-\theta)=2, \theta \in\left(\frac{\pi}{2}, \pi\right)$.
(1)求 $\sin \theta, \cos \theta$ 的值;
(2)求$\frac{4 \cos \left(\frac{\pi}{2}-\theta\right)-\sin \left(\frac{3 \pi}{2}+\theta\right)}{3 \sin (\pi-\theta)+5 \cos (2 \pi-\theta)}$ 的值.
对于函数 $f(x)$, 若在其定义域内存在实数 $x_{0}, t$, 使得 $f\left(x_{0}+t\right)=f\left(x_{0}\right)+f(t)$ 成立, 则称 $f(x)$ 是 “ $t$ 跃点”函数, 并称 $x_{0}$ 是函数 $f(x)$ 的 1 个 “ $t$ 跃点”.
(1) 求证:函数 $f(x)=2^{x}+2 x^{2}$ 在 $[0,1]$ 上是 “ 1 跃点” 函数;
(2) 若函数 $g(x)=x^{3}+\frac{1}{2} a x^{2}-3$ 在 $(-2,+\infty)$ 上存在 2 个 “ 1 跃点”, 求实数 $a$ 的取值范围;
(3) 是否同时存在实数 $m$ 和正整数 $n$ 使得函数 $h(x)=\cos 2 x-m$ 在 $[0, n \pi]$ 上有 2022 个 “隶跃 点” ? 若存在, 请求出 $m$ 和 $n$ 满足的条件, 若不存在, 请说明理由.
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
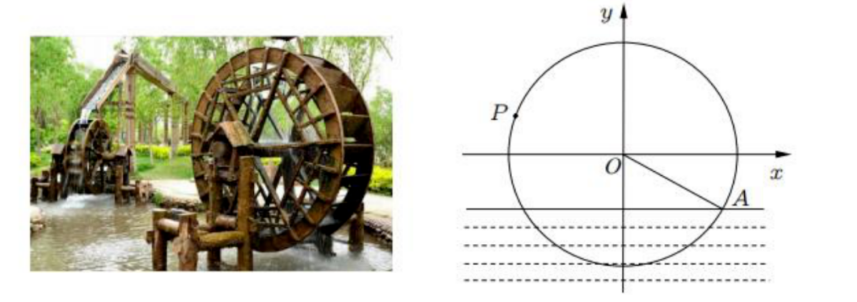
水车在古代是进行灌溉引水的工具, 是人类的一项古老的发明, 也是人类利用自然和改 造自然的象征. 如图一个半径为 $R \mathrm{~m}$ 的水车, 当水车上水斗 $A$ 从水中浮现时开始计算时间, 点 $A$ 沿圆周按逆时针方向匀速旋转, 且旋转一周用时 60 秒, 经过 $t$ 秒后, 水斗旋转到点 $P$, 已知 $A(2 \sqrt{3},-2)$, 设点 $P$ 的坐标为 $(x, y)$, 歩纵坐标满足 $y=f(t)=R \sin (\omega t+\varphi)(t \geqslant 0, \omega>\left.0,|\varphi| < \frac{\pi}{2}\right)$.
(1) 求函数 $f(t)$ 的解析式;
(2)当水车转动一圈时, 求点 $P$ 到水面的距离不低于 $4 \mathrm{~m}$ 的持续时间.
已知函数 $f(x)=\log _{2}\left(\frac{2}{x-1}+1\right), g(x)=-2^{x+1}$.
(1)求证: $f(x)$ 为奇函数;
(2)若 $2^{f\left(2^{*}\right)}-k \geqslant g(x)$ 恒成立, 求实数 $k$ 的取值范围;
(3) 解关于 $a$ 的不等式 $g(a)-g(2-a) \leqslant 2 a-2$.
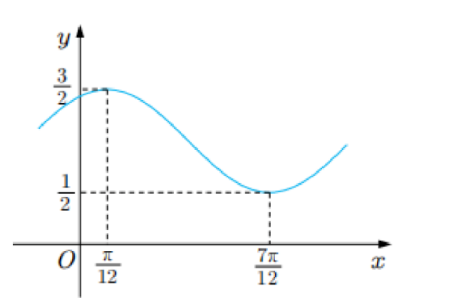
已知函数 $f(x)=A \sin (\omega x+\varphi)+B\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的部分图象如图所示.
(1) 求函数 $f(x)$ 的解析式;
(2) 将函数 $y=f(x)$ 的图象上所有的点向右平移 $\frac{\pi}{12}$ 个单位, 再将所得图象上每一个点的横坐标 变为原来的 2 倍(纵坐标不变), 得到函数 $y=g(x)$ 的图象.
(1)当 $x \in\left[-\frac{\pi}{3}, \frac{\pi}{2}\right]$ 时, 求函数 $g(x)$ 的值域;
(2)若方程 $g(x)-m=0$ 在 $\left[0, \frac{7 \pi}{3}\right]$ 上有三个不相等的实数根 $x_{1}, x_{2}, x_{3}\left(x_{1} < x_{2} < x_{3}\right)$, 求 $\tan \left(x_{1}\right.$ $\left.+2 x_{2}+x_{3}\right)$ 的值.