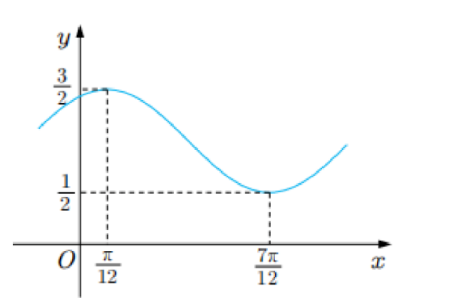
已知函数 $f(x)=A \sin (\omega x+\varphi)+B\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的部分图象如图所示.
(1) 求函数 $f(x)$ 的解析式;
(2) 将函数 $y=f(x)$ 的图象上所有的点向右平移 $\frac{\pi}{12}$ 个单位, 再将所得图象上每一个点的横坐标 变为原来的 2 倍(纵坐标不变), 得到函数 $y=g(x)$ 的图象.
(1)当 $x \in\left[-\frac{\pi}{3}, \frac{\pi}{2}\right]$ 时, 求函数 $g(x)$ 的值域;
(2)若方程 $g(x)-m=0$ 在 $\left[0, \frac{7 \pi}{3}\right]$ 上有三个不相等的实数根 $x_{1}, x_{2}, x_{3}\left(x_{1} < x_{2} < x_{3}\right)$, 求 $\tan \left(x_{1}\right.$ $\left.+2 x_{2}+x_{3}\right)$ 的值.