水车在古代是进行灌溉引水的工具, 是人类的一项古老的发明, 也是人类利用自然和改 造自然的象征. 如图一个半径为
(1) 求函数
(2)当水车转动一圈时, 求点
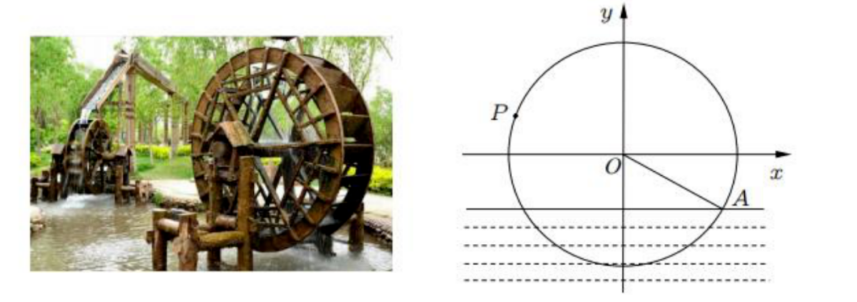
(1) 求函数
(2)当水车转动一圈时, 求点
