单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \mid x^{2}-2 x>0\right\}, B=\{x \mid-\sqrt{5} < x < \sqrt{5}\}$, 则( )
$\text{A.}$ $A \cap B=\emptyset$
$\text{B.}$ $A \cup B=R$
$\text{C.}$ $\mathrm{B} \subseteq \mathrm{A}$
$\text{D.}$ $A \subseteq B$
若复数 $z$ 满足 (3- $4 i) z=|4+3 i|$, 则 $z$ 的虚部为( )
$\text{A.}$ $-4$
$\text{B.}$ $-\frac{4}{5}$
$\text{C.}$ 4
$\text{D.}$ $\frac{4}{5}$
为了解某地区中小学生的视力情况, 拟从该地区的中小学生中抽取 部分学生进行调查, 事先已经了解到该地区小学、初中、高中三个学段学生 的视力情况有较大差异, 而男女生视力情况差异不大. 在下面的抽样方法中, 最合理的抽样方法是()
$\text{A.}$ 简单的随机抽样
$\text{B.}$ 按性别分层抽样
$\text{C.}$ 按学段分层抽样
$\text{D.}$ 系统抽样
已知双曲线 $c: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的离心率为 $\frac{\sqrt{5}}{2}$, 则 $c$ 的渐 近线方程为 ( )
$\text{A.}$ $y=\pm \frac{1}{4} x$
$\text{B.}$ $y=\pm \frac{1}{3} x$
$\text{C.}$ $y=\pm x$
$\text{D.}$ $y=\pm \frac{1}{2} x$
执行程序框图, 如果输入的 $ \mathrm{t} \in[-1,3] $ 则输出的 $\mathrm{s} $ 属于( )
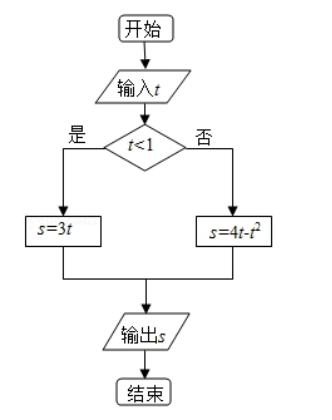
$\text{A.}$ $[-3,4]$
$\text{B.}$ $[-5,2]$
$\text{C.}$ $[-4,3]$
$\text{D.}$ $[-2,5]$
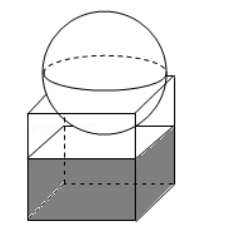
如图, 有一个水平放置的透明无盖的正方体容器, 容器高 $8 \mathrm{~cm}$, 将 一个球放在容器口, 再向容器注水, 当球面恰好接触水面时测得水深为 $6 \mathrm{~cm}$, 如不计容器的厚度, 则球的体积为 ( )
$\text{A.}$ $\frac{500 \pi}{3} \mathrm{~cm}^{3}$
$\text{B.}$ $\frac{866 \pi}{3} \mathrm{~cm}^{3}$
$\text{C.}$ $\frac{1372 \pi}{3} \mathrm{~cm}^{3}$
$\text{D.}$ $\frac{2048 \pi}{3} \mathrm{~cm}^{3}$
设等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 若 $S_{m-1}=-2, S_{m}=0, S_{m+1}=3$, 则 $m=$ ( )
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
某几何体的三视图如图所示,则该几何体的体积为( )
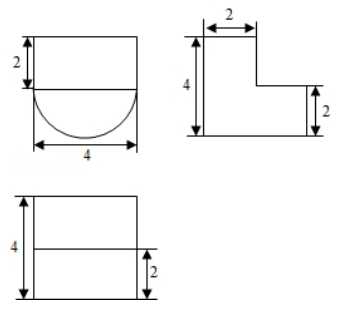
$\text{A.}$ $16+8 \pi$
$\text{B.}$ $8+8 \pi$
$\text{C.}$ $16+16 \pi$
$\text{D.}$ $8+16 \pi$
设 $m$ 为正整数, $(x+y)^{2 m}$ 展开式的二项式系数的最大值为 $a,(x+y )^{2m+1}$ 展开式的二项式系数的最大值为 $b$, 若 $13 a=7 b$, 则 $m=(\quad)$
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 7
$\text{D.}$ 8
已知椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的右焦点为 $F(3,0)$, 过点 $F$ 的直线交椭圆 $E$ 于 $A 、 B$ 两点. 若 $A B$ 的中点坐标为 $(1,-1)$, 则 $E$ 的方程 为 ( )
$\text{A.}$ $\frac{x^{2}}{45}+\frac{y^{2}}{36}=1$
$\text{B.}$ $\frac{x^{2}}{36}+\frac{y^{2}}{27}=1$
$\text{C.}$ $\frac{x^{2}}{27}+\frac{y^{2}}{18}=1$
$\text{D.}$ $\frac{x^{2}}{18}+\frac{y^{2}}{9}=1$
已知函数 $f(x)=\left\{\begin{array}{ll}-x^{2}+2 x, & x \leqslant 0 \\ \ln (x+1), & x>0\end{array}\right.$ 若 $|f(x)| \geqslant a x$, 则 $a$ 的取值 范围是()
$\text{A.}$ $(-\infty, 0]$
$\text{B.}$ $(-\infty, 1]$
$\text{C.}$ $[-2,1]$
$\text{D.}$ $[-2,0]$
设 $\triangle A_{n} B_{n} C_{n}$ 的三边长分别为 $a_{n}, b_{n}, c_{n}, \triangle A_{n} B_{n} C_{n}$ 的面积为 $S_{n}, n=1$ , 2, 3...若 $b_{1}>c_{1}, b_{1}+c_{1}=2 a_{1}, a_{n+1}=a_{n}, b_{n+1}=\frac{c_{n}+a_{n}}{2}, c_{n+1}=\frac{b_{n}+a_{n}}{2}$, 则 ( )
$\text{A.}$ $\left\{\mathrm{S}_{\mathrm{n}}\right\}$ 为递减数列
$\text{B.}$ $\left\{\mathrm{S}_{\mathrm{n}}\right\}$ 为递增数列
$\text{C.}$ $\left\{\mathbf{S}_{2 n-1}\right\}$ 为递增数列, $\left\{\mathbf{S}_{2 n}\right\}$ 为递减数列
$\text{D.}$ $\left\{\mathrm{S}_{2 \mathrm{n}-1}\right\}$ 为递减数列, $\left\{\mathrm{S}_{2 \mathrm{n}}\right\}$ 为递增数列
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知两个单位向量 $\vec{a}, \vec{b}$ 的夹角为 $60^{\circ}, \vec{c}=t \vec{a}+(1-t) \vec{b}$. 若 $\vec{b} \bullet \vec{c}=0$, 则 $\mathrm{t}=$.
若数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}=\frac{2}{3} a_{n}+\frac{1}{3}$, 则数列 $\left\{a_{n}\right\}$ 的通项公式是
设当 $x=\theta$ 时,函数 $f(x)=\sin x-2 \cos x$ 取得最大值, 则 $\cos \theta=$
若函数 $f(x)=\left(1-x^{2}\right)\left(x^{2}+a x+b\right)$ 的图象关于直线 $x=-2$ 对称, 则 $f(x)$ 的最大值为
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
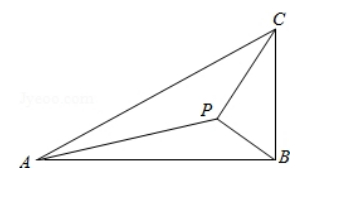
如图, 在 $\triangle \mathrm{ABC}$ 中, $\angle \mathrm{ABC}=90^{\circ}, \mathrm{AB}=\sqrt{3}, \mathrm{BC}=1, \mathrm{P}$ 为 $\triangle \mathrm{ABC}$ 内一 点, $\angle B P C=90^{\circ}$.
(1)若 $P B=\frac{1}{2}$, 求 $P A$;
(2) 若 $\angle \mathrm{APB}=150^{\circ}$, 求 $\tan \angle \mathrm{PBA}$.
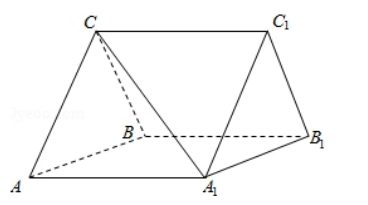
如图, 三棱柱 $\mathrm{ABC}-\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ 中, $\mathrm{CA}=\mathrm{CB}, \mathrm{AB}=\mathrm{AA}_{1}, \angle \mathrm{BAA}=60^{\circ}$.
(I) 证明 $A B \perp A_{1} C$;
(II) 若平面 $A B C \perp$ 平面 $A_{1} B_{1} B, A B=C B=2$, 求直线 $A_{1} C$ 与平面 $B_{1} C_{1} C$ 所成角的 正弦值.
一批产品需要进行质量检验, 检验方案是: 先从这批产品中任取 4 件作检验, 这 4 件产品中优质品的件数记为 $n$. 如果 $n=3$, 再从这批产品中任 取 4 件作检验, 若都为优质品, 则这批产品通过检验 如果 $n=4$, 再从这批产 品中任取 1 件作检验, 若为优质品, 则这批产品通过检验; 其他情况下, 这批产品都不能通过检验. 假设这批产品的优质品率为 $50 \%$, 即取出的产品是 优质品的概率都为 $\frac{1}{2}$, 且各件产品是否为优质品相互独立.
(I) 求这批产品通过检验的概率;
(II ) 已知每件产品检验费用为 100 元, 凡抽取的每件产品都需要检验, 对这批 产品作质量检验所需的费用记为 $\mathrm{X}$ (单位: 元), 求 $\mathrm{X}$ 的分布列及数学期望.
已知圆 $M:(x+1)^{2}+y^{2}=1$, 圆 $N:(x-1)^{2}+y^{2}=9$, 动圆 $P$ 与圆 $M$ 外切并与圆 $N$ 内切, 圆心 $P$ 的轨迹为曲线 $C$.
(I ) 求 C 的方程;
(II) $\mathrm{I}$ 是与圆 $\mathrm{P}$, 圆 $\mathrm{M}$ 都相切的一条直线, $\mathrm{I}$ 与曲线 $C$ 交于 $A, B$ 两点, 当圆 $P$ 的半径最长时, 求 $|A B|$.
已知函数 $f(x)=x^{2}+a x+b, g(x)=e^{x}(c x+d)$, 若曲线 $y=f(x)$ 和 曲线 $y=g(x)$ 都过点 $P(0,2)$, 且在点 $P$ 处有相同的切线 $y=4 x+2$.
(I) 求 $a, b, c, d$ 的值;
(II) 若 $x \geqslant-2$ 时, $f(x) \leqslant k g(x)$, 求 $k$ 的取值范围.
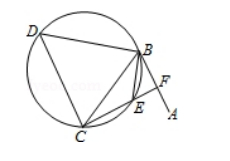
如图, 直线 $A B$ 为圆的切线, 切点为 $B$, 点 $C$ 在圆上, $\angle A B C$ 的角平分线 $B E$ 交圆 于点 $E, D B$ 垂直 $B E$ 交圆于 $D$.
(I ) 证明: DB=DC;
(II) 设圆的半径为 $1, B C=\sqrt{3}$, 延长 $C E$ 交 $A B$ 于点 $F$, 求 $\triangle B C F$ 外接圆的半径.
已知曲线 $C_{1}$ 的参数方程为 $\left\{\begin{array}{l}x=4+5 \cos t \\ y=5+5 \sin t\end{array}\right.$ ( $t$ 为参数), 以坐标原点为极点, $x$ 轴的正半轴为极轴建立极坐标系, 曲线 $C_{2}$ 的极坐标方程为 $\rho=2 \sin \theta$.
(1) 把 $C_{1}$ 的参数方程化为极坐标方程;
(2) 求 $C_{1}$ 与 $C_{2}$ 交点的极坐标 $(\rho \geqslant 0,0 \leqslant \theta < 2 \pi)$.
已知函数 $\mathrm{f}(\mathrm{x})=|2 \mathrm{x}-1|+|2 \mathrm{x}+\mathrm{a}|, \mathrm{g}(\mathrm{x})=\mathrm{x}+3$.
(I)当 $a=-2$ 时, 求不等式 $f(x) < g(x)$ 的解集;
(II ) 设 $a>-1$, 且当 $x \in\left[-\frac{a}{2}, \frac{1}{2}\right]$ 时, $f(x) \leqslant g(x)$, 求 $a$ 的取值范围.