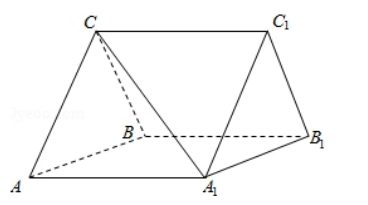
如图, 三棱柱 $\mathrm{ABC}-\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ 中, $\mathrm{CA}=\mathrm{CB}, \mathrm{AB}=\mathrm{AA}_{1}, \angle \mathrm{BAA}=60^{\circ}$.
(I) 证明 $A B \perp A_{1} C$;
(II) 若平面 $A B C \perp$ 平面 $A_{1} B_{1} B, A B=C B=2$, 求直线 $A_{1} C$ 与平面 $B_{1} C_{1} C$ 所成角的 正弦值.
(I) 证明 $A B \perp A_{1} C$;
(II) 若平面 $A B C \perp$ 平面 $A_{1} B_{1} B, A B=C B=2$, 求直线 $A_{1} C$ 与平面 $B_{1} C_{1} C$ 所成角的 正弦值.
