单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $M=\left\{x \mid \log _2 x < 1\right\}$, 集合 $N=\{x \mid-1 < x < 1\}$, 则 $M \bigcup N=$
$\text{A.}$ $(0,1)$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $(0,2)$
$\text{D.}$ $(-\infty, 2)$
2022 年三九天从农历腊月十八开始计算, 也就是 2023 年 1 月 9 日至 17 日, 是我 国北方地区一年中最冷的时间. 如图是北方某市三九天气预报气温图, 则下列对这 9 天判断 错误的是
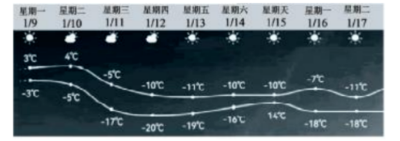
$\text{A.}$ 昼夜温差最大为 $12^{\circ} \mathrm{C}$
$\text{B.}$ 昼夜温差最小为 $4 \mathrm{C}$
$\text{C.}$ 有 3 天昼夜温差大于 $10^{\circ} \mathrm{C}$
$\text{D.}$ 有 3 天昼夜温差小于 $7^{\circ} \mathrm{C}$
已知 $\sin \theta+2 \cos ^2 \frac{\theta}{2}=\frac{5}{4}$, 则 $\sin 2 \theta=$
$\text{A.}$ $-\frac{15}{16}$
$\text{B.}$ $\frac{15}{16}$
$\text{C.}$ $-\frac{3}{4}$
$\text{D.}$ $\frac{3}{4}$
在 $\triangle A B C$ 中, $B C=2, \overrightarrow{A B} \cdot \overrightarrow{A C}=8$, 若 $D$ 是 $B C$ 的中点, 则 $A D=$
$\text{A.}$ 1
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
已知函数 $f(x)=\sin (\omega x+\varphi)\left(\omega>0,|\varphi| < \frac{\pi}{2}\right)$ 图象上相邻两条对称轴之间的距离为 $\frac{\pi}{2}$, 将函数 $y=f(x)$ 的图象向左平移 $\frac{\pi}{3}$ 个单位后, 得到的图象关于 $y$ 轴对称, 则函数 $f(x)$ 的一 个零点是
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{12}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{5 \pi}{12}$
已知 $\odot O, x^2+y^2=4, \odot C$ 与一条坐标轴相切, 圆心在直线 $x-y+7=0$ 上. 若 $\odot C$ 与 $\odot O$ 相切, 则满足条件的 $\odot C$ 有
$\text{A.}$ 1 个
$\text{B.}$ 2个
$\text{C.}$ 3 个
$\text{D.}$ 4 个
已知圆锥 $D O$ 的轴截面为等边三角形, $\triangle A B C$ 是底面 $\odot O$ 的内接正三角形, 点 $P$ 在 $D O$ 上, 且 $P O=\lambda D O$. 若 $P A \perp$ 平面 $P B C$, 则实数 $\lambda= $
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{6}}{3}$
$\text{C.}$ $\frac{\sqrt{6}}{4}$
$\text{D.}$ $\frac{\sqrt{6}}{6}$
已知动圆过定点 $M(0,4)$, 且在 $x$ 轴上截得的弦 $A B$ 的长为 8 . 过此动圆圆心轨迹 $C$ 上一个定点 $P(m, 2)$ 引它的两条弦 $P S, P T$, 若直线 $P S, P T$ 的倾斜角互为补角, 记直线 $S T$ 的斜率为 $k$, 则 $m k= $
$\text{A.}$ 4
$\text{B.}$ 2
$\text{C.}$ -4
$\text{D.}$ -2
多选题 (共 4 题 ),每题有多个选项正确
数列 $\left\{a_n\right\}$ 满足: $a_1=1, a_1+a_2+a_3+\ldots+a_{n-1}=4 a_n(n \geqslant 2)$, 则下列结论中正确的是
$\text{A.}$ $a_2=\frac{1}{4}$
$\text{B.}$ $a_{n+1}=\frac{5}{4} a_n, n \geqslant 2$
$\text{C.}$ $\left\{a_n\right\}$ 是等比数列
$\text{D.}$ $a_1+a_2+a_3+\ldots+a_n=\left(\frac{5}{4}\right)^{n-1}, n \in N^*$
已知 $e$ 是自然对数的底数, 则下列不等关系中正确的是
$\text{A.}$ $e^\pi>3^c$
$\text{B.}$ $\pi^\epsilon < e^\pi$
$\text{C.}$ $2^e < e^2$
$\text{D.}$ $e^3 < 3^e$
已知 $f(x)(x \in R)$ 为偶函数, 且 $f\left(x-\frac{3}{2}\right)=f\left(x+\frac{1}{2}\right)$ 恒成立. 当 $x \in[2,3]$ 时 $f(x)=x$. 则下列四个命題中, 正确的是
$\text{A.}$ $f(x)$ 的周期是 $2 k(k \neq 0, k \in Z)$
$\text{B.}$ $f(x)$ 的图象关于点 $(1,0)$ 对称
$\text{C.}$ 当 $x \in[-3,-2]$ 时, $f(x)=-x$
$\text{D.}$ 当 $x \in[-2,0]$ 时, $f(x)=3-|x+1|$
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $1, E, F$ 分别是棱 $A_1 D_1$ 和棱 $C_1 D_1$ 的中点, $G$ 为棱 $B C$ 上的动点 (不含端点). 下列说法中正确的是
$\text{A.}$ 当 $G$ 为棱 $B C$ 的中点时, $\triangle E F G$ 是锐角三角形
$\text{B.}$ 三棱雉 $D_1-E F G$ 的体积为定值
$\text{C.}$ $\triangle E F G$ 面积的取值范围是 $\left(\frac{3}{8}, \frac{\sqrt{17}}{8}\right)$
$\text{D.}$ 若异面直线 $A B$ 与 $E G$ 所成的角为 $\alpha$, 则 $\sin \alpha \in\left[\frac{\sqrt{2}}{2}, \frac{\sqrt{5}}{3}\right.$ )
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若复数 $z=\frac{i}{2-i}$ ( $i$ 是虚数单位) 的共轭复数是 $\bar{z}$, 则 $z-\bar{z}$ 的虚部是
2022 年 12 月 18 日在卡塔尔世界杯决赛中, 阿根廷队以总分 7 比 5 战胜法国队, 历时 28 天的 2022 卡塔尔世界杯也缓缓落下了帷幕. 随后某电视台轮流播放半决赛及以后的 这 4 场足球赛 (如图), 某人随机选 3 场进行观看, 其中恰好总决赛、季军赛被选上的概率 为
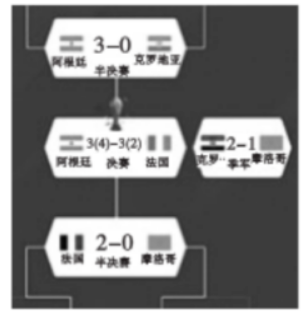
过点 $A(0,1)$ 作斜率为 $k$ 的直线 $l$ 交双曲线 $x^2-\frac{y^2}{2}=1$ 于 $P_1, P_2$ 两点, 线段 $P_1 P_2$ 的 中点在直线 $x=\frac{1}{2}$ 上, 则实数 $k$ 的值为
已知直线 $l$ 与曲线 $y=e^x 、 y=2+\ln x$ 都相切, 则直线 $l$ 的方程为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在锐角 $\triangle A B C$ 中, $B C$ 在 $A B$ 上的投影长等于 $\triangle A B C$ 的外接圆半径 $R$.
(1) 求 $\sin A \cos B$ 的值;
(2) 若 $4 \cos A \sin B=1$, 且 $A B=3$, 求 $R$.
2022 年北京冬奥会圆满落幕, 随后多所学校掀起了 “雪上运动” 的热潮. 为了 解学生对 “雪上运动” 的喜爱程度, 某学校从全校学生中随机抽取 200 名学生进行问卷调查, 得到以下数据:
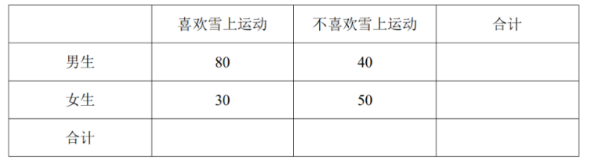
(1) 完成 $2 \times 2$ 列联表, 依据小概率值 $\alpha=0.01$ 的 $\chi^2$ 独立性检验, 能否认为是否喜欢雪上运 动与性别有关联?
(2) (i) 从随机抽取的这 200 名学生中采用分层抽样的方法抽取 20 人, 再从这 20 人中随机抽取 3 人. 记事件 $A=$ “至少有 2 名是男生”, 事件 $B=$ “至少有 2 名喜欢雪上运动的 男生”, 事件 $C=$ “至多有 1 名喜欢雪上运动的女生”. 试计算 $P(\mathrm{~A}) \cdot P(B \mid A) \cdot P(C \mid A B)$ 和 $P(A B C)$ 的值, 并比较它们的大小.
(ii) ( i ) 中 $P(A B C)$ 与 $P(\mathrm{~A}) \cdot P(B \mid A) \cdot P(C \mid A B)$ 的大小关系能否推广到更一般的情形? 请写出结论, 并说明理由.
参考公式及数据 $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}, n=a+b+c+d$.

已知数列 $\left\{a_n\right\}$ 的各项均为正数, 其前 $n$ 项和为 $S_n$, 且 $a_n^2-2 S_n \cdot a_n+1=0$.
(1) 求 $a_n$ 和 $S_n$;
(2) 若 $n \geqslant 3$, 证明: $\frac{1}{S_1^2}+\frac{1}{S_2^2}+\ldots+\frac{1}{S_n^2}>2\left(1-\frac{1}{2^4}\right)$.
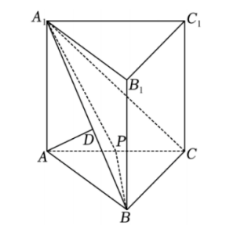
20. (12 分) 如图, 在直三棱柱 $A B C-A_1 B_1 C_1$ 中, $D$ 为 $A_1 B$ 上一点, $A D \perp$ 平面 $A_1 B C$.
(1) 求证: $B C \perp A_1 B$;
(2) 若 $A D=\sqrt{3}, A B=B C=2, P$ 为 $A C$ 的中点, 求二面角 $A-A, B-P$ 的余弦值.
已知 $F_1, F_2$ 为椭圆 $C: \frac{x^2}{2}+y^2=1$ 的左右焦点, $P$ 为椭圆 $C$ 上一点. 若 $\triangle P F_1 F_2$ 为直角三角形, 且 $\left|P F_1\right| \geqslant\left|P F_2\right|$.
(1) 求 $\frac{\left|P F_1\right|}{\left|P F_2\right|}$ 的值;
(2) 若直线 $l: y=k x+m(k \neq 0)$ 与椭圆 $C$ 交于 $A, B$ 两点, 线段 $A B$ 的垂直平分线经过点 $N\left(0,-\frac{1}{2}\right)$, 求实数 $m$ 的取值范围.
已知函数 $f(x)=e^x+a \cos x$, 其中 $x>0, a \in R$.
(1) 当 $a=-1$ 时, 讨论 $f(x)$ 的单调性;
(2) 若函数 $f(x)$ 的导函数 $f^{\prime}(x)$ 在 $(0, \pi)$ 内有且仅有一个极值点, 求 $a$ 的取值范围.