单选题 (共 8 题 ),每题只有一个选项正确
若复数 $z$ 满足 $(1+\mathrm{i}) z=|1+\mathrm{i}|$, 则 $z$ 的虚部为()
$\text{A.}$ $-\frac{\sqrt{2}}{2} i$
$\text{B.}$ $-\frac{\sqrt{2}}{2}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $-\sqrt{2}$
已知全集 $U=A \cup B=(0,2], A \cap C_{U} B=(1,2]$, 则 $B=(\quad)$
$\text{A.}$ $(0,1]$
$\text{B.}$ $(0,2)$
$\text{C.}$ $(0,1)$
$\text{D.}$ $\varnothing$
某密码锁的一个密码由 3 位数字组成, 每一位均可取 $0,1,2, \ldots, 9$ 这 10 个数字中的一个, 小明随机 设置了一个密码, 则恰有两个位置数字相同的概率为( )

$\text{A.}$ $0.09$
$\text{B.}$ $0.12$
$\text{C.}$ $0.18$
$\text{D.}$ $0.27$
若 $3^{x}=4^{y}=10, z=\log _{x} y$, 则
$\text{A.}$ $x>y>z$
$\text{B.}$ $y>x>z$
$\text{C.}$ $z>x>y$
$\text{D.}$ $x>z>y$
若 $(2 x+1)^{n}$ 的展开式中 $x^{3}$ 项的系数为 160 , 则正整数 $n$ 的值为 ( )
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
在平面直角坐标系 $x O y$ 中,角 $\theta$ 的大小如图所示,则 $9 \sin ^{2} \theta+\sin 2 \theta=$
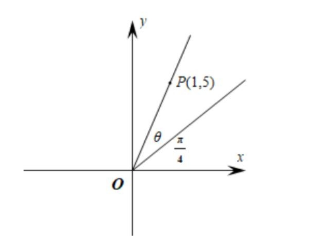
$\text{A.}$ $1$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{48}{13}$
$\text{D.}$ $\frac{5}{2}$
在平面直角坐标系 $x O y$ 中, 抛物线 $C: x^{2}=2 p y(p>0)$ 的焦点为 $F, P$ 是 $C$ 上位于第一象限内的一点, 若 $C$ 在点 $P$ 处的切线与 $x$ 轴交于 $M$ 点, 与 $y$ 轴交于 $N$ 点, 则与 $|P F|$ 相等的是()
$\text{A.}$ $|M N|$
$\text{B.}$ $|F N|$
$\text{C.}$ $|P M|$
$\text{D.}$ $|O N|$
已知函数 $f(x)=x-\frac{1}{x}-2 \ln x$, 当 $x>1$ 时, $f\left(x^{2}\right)>8 \lambda f(x)$ 恒成立, 则实数 $\lambda$ 的取值范围为( )
$\text{A.}$ $(-\infty,-2]$
$\text{B.}$ $(-\infty, 2]$
$\text{C.}$ $(-\infty,-1]$
$\text{D.}$ $(-\infty, 1]$
多选题 (共 4 题 ),每题有多个选项正确
已知函数 $f(x)=0.5^{\sin x+\cos x}$, 则 ( )
$\text{A.}$ $f(x)$ 是以 $2 \pi$ 为周期的周期函数
$\text{B.}$ 直线 $x=\frac{3 \pi}{4}$ 是 $f(x)$ 图象的一条对称轴
$\text{C.}$ $f(x)$ 的值域为 $\left[2^{-\sqrt{2}}, 2^{\sqrt{2}}\right]$
$\text{D.}$ $f(x)$ 在 $\left[\pi, \frac{5 \pi}{4}\right]$ 上单调递增
折扇是我国古老文化的延续, 在我国已有四千年左右的历史, “扇”与“善”谐音, 折扇也寓意“善良”“善 行”. 它常以字画的形式体现我国的传统文化, 也是运筹帷幄, 决胜千里, 大智大勇的象征 (如图 1). 图 2 是一个圆台的侧面展开图(扇形的一部分), 若两个圆弧 $\overparen{D E}, \overparen{A C}$ 所在圆的半径分别是 3 和 9 , 且 $\angle A B C=120^{\circ}$, 则该圆台的()
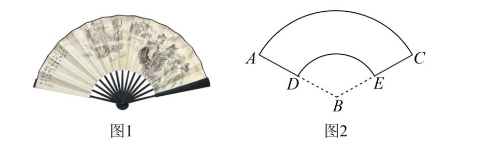
$\text{A.}$ 高为 $4 \sqrt{2}$
$\text{B.}$ 体积为 $\frac{50 \sqrt{2}}{3} \pi$
$\text{C.}$ 表面积为 $34 \pi$
$\text{D.}$ 上底面积、下底面积和侧面积之比为 $1: 9: 22$
已知 $S_{n}$ 是数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, 且 $a_{1}=1, a_{2}=5, a_{n+2}=2 a_{n+1}+8 a_{n}$, 则
$\text{A.}$ 数列 $\left\{a_{n+1}-4 a_{n}\right\}$ 为等比数列
$\text{B.}$ 数列 $\left\{a_{n+1}+2 a_{n}\right\}$ 为等比数列
$\text{C.}$ $a_{9}=\frac{7 \times 4^{8}+2^{8}}{6}$
$\text{D.}$ $S_{9}=\frac{7 \times 4^{9}-2^{9}-5}{18}$
已知双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的右焦点为 $F$, 左、右顶点分别为 $A_{1}, A_{2}$, 则 ( )
$\text{A.}$ 过点 $A_{2}$ 与 $C$ 只有一个公共点的直线有 2 条
$\text{B.}$ 若 $C$ 的离心率为 $\sqrt{5}$, 则点 $F$ 关于 $C$ 的渐近线的对称点在 $C$ 上
$\text{C.}$ 过 $F$ 的直线与 $C$ 右支交于 $M, N$ 两点, 则线段 $M N$ 的长度有最小值
$\text{D.}$ 若 $C$ 为等轴双曲线, 点 $P$ 是 $C$ 上异于顶点的一点, 且 $\left|A_{1} A_{2}\right|=\left|P A_{2}\right|$, 则 $\angle P A_{1} A_{2}=\frac{\pi}{6}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $\triangle A B C$ 是边长为 1 的等边三角形, 设向量 $\vec{a}, \vec{b}$ 满足 $\overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{a}+\vec{b}$, 则 $|3 \vec{a}+\vec{b}|=$
若函数 $f(x)=a^{x}+b^{x}(a>0, b>0, a \neq 1, b \neq 1)$ 是偶函数, 则 $\frac{1}{a}+\frac{4}{b}$ 的最小值为
利用分层随机抽样的方法, 调研某校高二年级学生某次数学测验的成绩(满分 100 分), 获得样本数据 的特征量如下表:
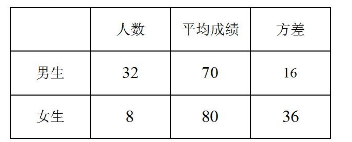
则总样本的平均分为 ( ) , 方差为 ( )
参考公式: $n$ 个数 $x_{1}, x_{2}, x_{3}, \cdots, x_{n}$ 的平均数为 $\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}$, 方差为
$$
s^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{n}\left[\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)-n \bar{x}^{2}\right]
$$
参考数据: $8 \times\left(36+80^{2}\right)+32 \times\left(16+70^{2}\right)-40 \times 72^{2}=1440$.
在直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 中, $A A_{1}=2, A B=\sqrt{3}$, 平面 $\alpha$ 经过点 $\mathrm{A}$, 且满足直线 $A A_{1}$ 与平面 $\alpha$ 所成 的角为 $30^{\circ}$, 过点 $A_{1}$ 作平面 $\alpha$ 的垂线, 垂足为 $H$, 则 $B H$ 长度的取值范围为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在①$a_{1}, a_{3}, a_{9}$ 成等比数列, ② $\frac{S_{n}}{a_{n}}=\frac{n+1}{2}$, ③ $S_{6}=2 S_{4}+4$ 这三个条件中任选一个, 补充在下面问题中, 并完成解答.
问题: 在公差不为 0 的等差数列 $\left\{a_{n}\right\}$ 中, 其前 $n$ 项和为 $S_{n}, a_{4}=16$ ,是否存在正整数 $k$, 使 得 $S_{k} < 2 a_{k}+20$ ? 若存在, 求出所有的正整数 $k$; 若不存在, 请说明理由.
18. 在平面四边形 $A B C D$ 中, 对角线 $A C$ 与 $B D$ 交于点 $E, \angle A B D=45^{\circ}, A E=E C, D E=2 B E, A B=6$,
$$
A D=3 \sqrt{2} .
$$
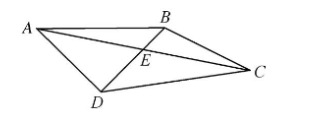
(1)求 $A C$ 的长;
(2) 求 $\sin \angle A D C$ 的值.
某省为调査北部城镇 2021 年国民生产总值, 抽取了 20 个城镇进行分析, 得到样本数据 $\left(x_{i}, y_{i}\right)(i=1,2$,
$\cdots, 20$ ), 其中 $x_{i}$ 和 $y_{i}$ 分别表示第 $\mathrm{i}$ 个城镇的人口 (单位: 万人) 和该城镇 2021 年国民生产总值(单位: 亿 元), 计算得 $\sum_{i=1}^{20} x_{i}=100, \sum_{i=1}^{20} y_{i}=800, \sum_{i=1}^{20}\left(x_{i}-\bar{x}\right)^{2}=70, \sum_{i=1}^{20}\left(y_{i}-\bar{y}\right)^{2}=280, \sum_{i=1}^{20}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)=120$.
(1) 请用相关系数 $r$ 判断该组数据中 $y$ 与 $x$ 之间线性相关关系的强弱 (若 $|r| \in[0.75,1]$, 相关性较强; 若
$|r| \in[0.30,0.75)$, 相关性一般; 若 $r \in[-0.25,0.25]$, 相关性较弱);
(2) 求 $y$ 关于 $x$ 的线性回归方程;
(3) 若该省北部某城镇 2021 年的人口约为 5 万人, 根据(2)中的线性回归方程估计该城镇 2021 年的国 民生产总值.
参考公式: 相关系数 $r=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}$, 对于一组具有线性相关关系的数据 $\left(x_{i}, y_{i}\right)(i=1,2, \cdots, n)$, 其回归直线 $\hat{y}=\hat{b} x+\hat{a}$ 的斜率和截距的最小二乘估计分别为
$$
\hat{b}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}, \quad \hat{a}=\bar{y}-\hat{b} \bar{x}
$$
如图, 在直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 中, $A C \perp B C, A C=B C=2, C C_{1}=3$, 点 $D, E$ 分别在棱 $A A_{1}$ 和棱 $C C_{1}$ 上, 且 $A D=1, C E=2$.
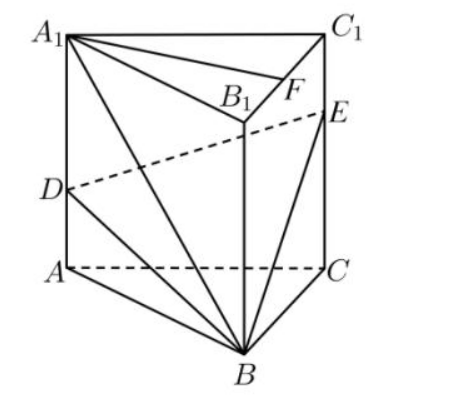
(1) 设 $F$ 为 $B_{1} C_{1}$ 中点, 求证: $A_{1} F / /$ 平面 $B D E$;
(2) 求直线 $A_{1} B_{1}$ 与平面 $B D E$ 所成角的正弦值.
已知椭圆 $C$ 的焦点为 $F_{1}(-\sqrt{2}, 0), F_{2}(\sqrt{2}, 0)$, 且 $C$ 过点 $E(\sqrt{2}, 1)$.
(1) 求 $C$ 的方程;
(2) 设 $\mathrm{A}$ 为椭圆 $C$ 的右顶点, 直线 $l$ 与椭圆 $C$ 交于 $P, Q$ 两点, 且 $P, Q$ 均不是 $C$ 的左, 右顶点, $M$ 为 $P Q$ 的
中点. 若 $\frac{|A M|}{|P Q|}=\frac{1}{2}$, 试探究直线 $l$ 是否过定点? 若过定点, 求出该定点坐标; 若不过定点, 请说明理由.
已知 $a \geqslant 0$, 函数 $f(x)=a x+\frac{1+a}{x}-\ln x$.
(1) 讨论函数 $f(x)$ 的单调性;
(2)如果我们用 $n-m$ 表示区间 $(m, n)$ 的长度, 试证明: 对任意实数 $a \geqslant 1$, 关于 $x$ 的不等式 $f(x) < 2 a+1$ 的解集的区间长度小于 $2 a+1$.