利用分层随机抽样的方法, 调研某校高二年级学生某次数学测验的成绩(满分 100 分), 获得样本数据 的特征量如下表:
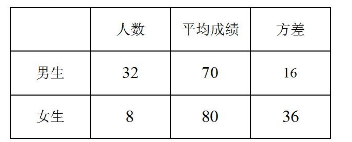
则总样本的平均分为 ( ) , 方差为 ( )
参考公式: $n$ 个数 $x_{1}, x_{2}, x_{3}, \cdots, x_{n}$ 的平均数为 $\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}$, 方差为
$$
s^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{n}\left[\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)-n \bar{x}^{2}\right]
$$
参考数据: $8 \times\left(36+80^{2}\right)+32 \times\left(16+70^{2}\right)-40 \times 72^{2}=1440$.

则总样本的平均分为 ( ) , 方差为 ( )
参考公式: $n$ 个数 $x_{1}, x_{2}, x_{3}, \cdots, x_{n}$ 的平均数为 $\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}$, 方差为
$$
s^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{n}\left[\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)-n \bar{x}^{2}\right]
$$
参考数据: $8 \times\left(36+80^{2}\right)+32 \times\left(16+70^{2}\right)-40 \times 72^{2}=1440$.