单选题 (共 8 题 ),每题只有一个选项正确
倾斜角为 $120^{\circ}$ 的直线经过点 $(a+1,3)$ 和 $(2 a-2,3 a)$, 则 $a=$
$\text{A.}$ $-\sqrt{3}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $3$
$\text{D.}$ $-3$
椭圆 $\frac{x^2}{5}+\frac{y^2}{9}=1$ 上的一点到两个焦点的距离之和为
$\text{A.}$ $2 \sqrt{5}$
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 18
双曲线 $C: \frac{x^2}{36}-\frac{y^2}{13}=1$ 上的点 $P$ 到左焦点的距离为 10 , 则 $P$ 到右焦点的距离为
$\text{A.}$ 2
$\text{B.}$ 22
$\text{C.}$ 2 或 22
$\text{D.}$ 12
圆 $x^2+y^2-4 x=0$ 与圆 $(x-a)^2+(y+3)^2=9$ 佮有两条公切线, 则 $a$ 的取值范围是
$\text{A.}$ $(-2,6)$
$\text{B.}$ $(-4,4)$
$\text{C.}$ $(-5,5)$
$\text{D.}$ $(-6,6)$
已知直线 $l: \sqrt{3} x+y-2=0$, 则
$\text{A.}$ 直线 $l$ 的倾斜角为 $\frac{5 \pi}{6}$
$\text{B.}$ 直线 $l$ 的斜率为 $\sqrt{3}$
$\text{C.}$ 直线 $l$ 的一个法向車为 $\boldsymbol{u}=(1, \sqrt{3})$
$\text{D.}$ 直线 $l$ 的一个方向向㞷为 $\boldsymbol{v}=(-\sqrt{3}, 3)$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2, P$ 是右支上一点, 且 $|P F_1$ | $=6\left|P F_2\right|$, 则双曲线 $C$ 的离心率的取值范围是
$\text{A.}$ $\left(0, \frac{7}{5}\right]$
$\text{B.}$ $\left(1, \frac{4}{3}\right]$
$\text{C.}$ $\left(1, \frac{7}{5}\right]$
$\text{D.}$ $\left[\frac{7}{5},+\infty\right)$
如图, 已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分別为 $F_1, F_2$, 点 $M$ 与 $C$ 的焦点不 重合, 点 $M$ 关于 $F_1, F_2$ 的对称点分别为 $A, B$, 线段 $M N$ 的中点 $Q$ 在 $C$ 的右支上. 若 $|A N|-$ $|B N|=18$, 则 $C$ 的实轴长为
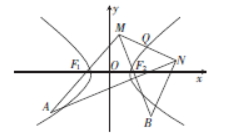
$\text{A.}$ 6
$\text{B.}$ 9
$\text{C.}$ 12
$\text{D.}$ 15
台风中心从 $M$ 地以每小时 $30 \mathrm{~km}$ 的速度向西北方向移动, 离台风中心 $30 \sqrt{3} \mathrm{~km}$ 内的地区为 危险地区,城市 $N$ 在 $M$ 地正西方向 $60 \mathrm{~km}$ 处, 则城市 $N$ 处于危险区内的时长为
$\text{A.}$ $1 \mathrm{~h}$
$\text{B.}$ $\sqrt{2} \mathrm{~h}$
$\text{C.}$ $2 \mathrm{~h}$
$\text{D.}$ $3 \mathrm{~h}$
多选题 (共 4 题 ),每题有多个选项正确
已知双曲线 $C: \frac{y^2}{4}-\frac{x^2}{6}=1$, 则
$\text{A.}$ 双曲线 $C$ 的焦点坐标为 $(0, \pm 2)$
$\text{B.}$ 双曲线 $C$ 的渐近线方程为 $y=\pm \frac{\sqrt{6}}{3} x$
$\text{C.}$ 双曲线 $C$ 的离心率为 $\frac{\sqrt{10}}{2}$
$\text{D.}$ 双曲线 $C$ 的虚轴长为 4
设直线 $l: a x+(2 a+3) y-3=0$ 与 $n:(a-2) x+a y-1=0$, 则
$\text{A.}$ 当 $a=-2$ 时, $l / / n$
$\text{B.}$ 当 $a=\frac{1}{3}$ 时, $l \perp n$
$\text{C.}$ 当 $l / / n$ 时, $l, n$ 间的距离为 $\frac{\sqrt{5}}{2}$
$\text{D.}$ 坐标原点到直线 $n$ 的距离的最大值为 $\frac{\sqrt{2}}{2}$
若关于 $x$ 的方程 $x+\sqrt{1-x^2}-b=0$ 有唯一解, 则 $b$ 的取值可能是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ 1
$\text{C.}$ $-\sqrt{2}$
$\text{D.}$ $\sqrt{2}$
历史上, 许多人研究过圆锥的截口曲线. 如图, 在圆锥中, 母线与旋转轴的夹角为 $\frac{\pi}{6}$, 现有一 截面与圆锥的一条母线垂直, 与旋转轴的交点 $O$ 到圆锥硕点的距离为 4 , 关于所得截口曲线, 下列选项正确的是
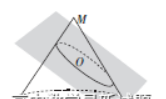
$\text{A.}$ 曲线形状为圆
$\text{B.}$ 曲线形状为椭圆
$\text{C.}$ 点 $O$ 为该曲线上距离最长的两点确定的线段的三等分点
$\text{D.}$ 该曲线上任意两点间的最长距离为 6
填空题 (共 4 题 ),请把答案直接填写在答题纸上
古希腊数学家阿基米德早在 2200 多年前利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积. 已知椭圆 $\frac{x^2}{28}+\frac{y^2}{7}=1$, 则该椭圆的面积为
过双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点作一条直线, 当直线的斜率为 $-1$ 时, 直线与双曲 线的左、右两支各有一个交点, 当直线的斜率为 $-\sqrt{3}$ 时, 直线与双曲线的左支有两个不同的 交点, 则双曲线的离心率可以为
已知圆 $C:(x+3)^2+(y-2)^2=4$, 则直线 $l: a x+y+2 a-1=0$ 被圆 $C$ 截得的弦长的最小 值为
一条沿直线传播的光线经过点 $P(-3,7)$ 和 $Q(-2,5)$, 然后被直线 $y=x-2$ 反射, 则人射点 的坐标为 ( ) , 反射光线所在直线在 $y$ 轴上的截距为 ( ).
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 的定点 $A(3,-4), A B$ 边上的中线所在直线的方程为 $x-2 y+4=0, A C$ 边上的 高所在直线的方程为 $x-y+2=0$.
(1)求 $C$ 的坐标;
(2)求直线 $B C$ 的方程.
曲线 $C$ 上任意一点到点 $M(-3,4)$ 的距离与到点 $N(-2,1)$ 的距离之比为 $\sqrt{2}$.
(1)试问曲线 $C$ 为何种曲线, 说明你的理由;
(2) 过直线 $l: x+y-5=0$ 上一点 $E$ 向曲线 $C$ 作一条切线, 切点为 $F$, 求 $|E F|$ 的最小值.
已知圆心为 $M$ 的圆经过 $A(-2,6), B(6,0), C(-8,-2)$ 这三个点.
(1) 求圆 $M$ 的标准方程;
(2) 直线 $l$ 过点 $P(4,6)$, 若直线 $l$ 被圆 $M$ 截得的弦长为 10 , 求直线 $l$ 的方程.
已知椭圆 $C_{:} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 㐫心率为 $\frac{\sqrt{3}}{3}$, 过点 $F_1$ 的直线 $l$ 交椭圆 $C$ 于 $A, B$ 两点, $A B$ 的中点坐标为 $\left(-\frac{12}{7}, \frac{4}{7}\right)$.
(1) 求椭圆 $C$ 的标准方程;
(2) 求 $\triangle A F_2 B$ 的面积.
已知椭圆 $C_{:} \frac{x^2}{a^2}+\frac{y^2}{a^2-4}=1(a>2)$ 过点 $\left(\frac{5}{4}, \frac{9}{4}\right), F_1, F_2$ 分别为左、右焦点, $P$ 为第一象限内 楉圆 $C$ 上的动点, 直线 $P F_1, P F_2$ 与直线 $x=t(t>0)$ 分別交于 $A, B$ 两点, 记 $\triangle P A B$ 和 $\triangle P F_1 F_2$ 的面积分别为 $S_1, S_2$.
(1) 试确定实数 $t$ 的值, 使得点 $P$ 到 $F_2$ 的距为与到直线 $x=t$ 的距㝑之比为定值 $k$, 并求出 $k$ 的值;
(2) 在 (1)的条件下, 若 $\frac{S_1}{S_2}=\frac{25}{9}$, 求 $\frac{|P A|\left|P F_1\right|}{P B\left|P F_2\right|}$ 的值.
已知双曲线 $C_: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2$, 实轴长为 $2 \sqrt{3}$, 一条渐近线方程为 $\sqrt{3} x-3 y=0$, 过 $F_2$ 的直线 $l$ 与双曲线 $C$ 的右支交于 $A, B$ 两点.
(1) 求双曲线 $C$ 的方程;
(12 已知$P(-\sqrt{5},0)$ 若三角形ABP的外心$Q$的横坐标为0,请直线l的方程