单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\left\{x \mid-1 < x < 3, x \in N^*\right\}, B=\{0,1,2,3\}$, 则 $A \cap B=$
$\text{A.}$ $\{1,2\}$
$\text{B.}$ $\{0,1,2\}$
$\text{C.}$ $\{0,1,2,3\}$
$\text{D.}$ $\{1,2,3\}$
已知复数 $z=\frac{1}{2}+\frac{\sqrt{3}}{2} \mathrm{i}$, 则 $\bar{z}+\frac{1}{z^2}=$
$\text{A.}$ $-\sqrt{3} i$
$\text{B.}$ $-\sqrt{3}$
$\text{C.}$ $1+\sqrt{3} i$
$\text{D.}$ $1-\sqrt{3} \mathrm{i}$
已知经过第一、二、四象限的直线 $l: \frac{x}{a}+\frac{y}{b}=1$ 经过点 $P(2,1)$, 则 $2 a+b$ 的最小值为
$\text{A.}$ $4$
$\text{B.}$ $4 \sqrt{2}$
$\text{C.}$ 8
$\text{D.}$ 9
若 $\tan \theta=2$, 则 $\frac{\sin \theta \cos 2 \theta}{\cos \theta-\sin \theta}=$
$\text{A.}$ $\frac{6}{5}$
$\text{B.}$ $-\frac{6}{5}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $-\frac{2}{5}$
现有 6 家商户预租赁某夜市的 6 个相邻的摊位, 其中 3 家商户开特色小吃店, 2 家商户开文 创产品店, 一家商户开新奇玩具店, 夜市管理部门要求特色小吃店必须都相邻, 且文创产 品店不相邻, 则不同的排法总数为
$\text{A.}$ 48
$\text{B.}$ 72
$\text{C.}$ 144
$\text{D.}$ 96
设 $F_1 、 F_2$ 分别是椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点, $P$ 为唨圆上的一点, 若 $\frac{\left|P F_2\right|}{\left|P F_1\right|^2+8\left|P F_2\right|^2}$ 的最大值为 $\frac{1}{8 a}$, 则椭圆的离心率的取值范围是
$\text{A.}$ $\frac{1}{3} \leq e < 1$
$\text{B.}$ $\frac{1}{3} < e < 1$
$\text{C.}$ $0 < e < \frac{1}{3}$
$\text{D.}$ $0 < e \leq \frac{1}{3}$
已知 $\triangle A B C$ 中, $\angle B=\frac{\pi}{6}, A C=2$, 则 $\angle A=\frac{\pi}{6}$ 的充要条件是
$\text{A.}$ $\triangle A B C$ 是等腰三角形
$\text{B.}$ $A B=2 \sqrt{3}$
$\text{C.}$ $B C=4$
$\text{D.}$ $S_{\triangle A B C}=\sqrt{3}, B C < B A$
已知函数 $f(x)$ 的定义域为 $R$, 且 $f(m+n)+f(m-n)=f(m) f(n), f(1)=1(m, n \in R)$, 则 $\sum_{i=1}^{20} f(i)=$
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ -2
$\text{D.}$ -3
多选题 (共 4 题 ),每题有多个选项正确
如图, 棱长为 4 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $E, F$ 分别为 $D D_1 、 B C$ 的中点, 下列结论正确的是
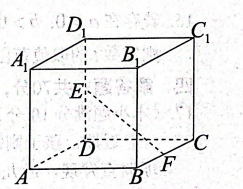
$\text{A.}$ $E F \perp A_1 D$
$\text{B.}$ 直线 $A E$ 与平面 $B_1 C D$ 所成角的正切值为 3
$\text{C.}$ $E F / /$ 平面 $A_1 B D_1$
$\text{D.}$ 平面 $A E F$ 截正方体 $A B C D-A_1 B_1 C_1 D_1$ 的截面周长为 $4 \sqrt{5}+2 \sqrt{6}$
已知数列 $\left\{a_n\right\}$ 满足 $a_n>0, \frac{a_{n+1}}{n}=\frac{a_n}{a_n^2+n-1}\left(n \in N^*\right)$, 数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 则下 列结论正确的是
$\text{A.}$ $a_1 a_2=1$
$\text{B.}$ $a_1=1$
$\text{C.}$ $S_{2020} \cdot a_{2021}=2020$
$\text{D.}$ $S_{2020} \cdot a_{2021}>2020$
已知函数 $f(x)=\sin (\omega x+\varphi)(\omega>0,0 < \varphi < \pi), f\left(\frac{\pi}{4}\right)=0$, 且对任意 $x \in R$ 均有 $f(x) \leq\left|f\left(\frac{\pi}{2}\right)\right|, f(x)$ 在 $\left[0, \frac{\pi}{2}\right]$ 上单调递减, 则下列说法正确的有
$\text{A.}$ 函数 $f(x)$ 为偶函数
$\text{B.}$ 函数 $f(x)$ 的最小正周期为 $2 \pi$
$\text{C.}$ 若 $f(x)=\frac{1}{3}(x \in[0,2 \pi])$ 的根为 $x_i(i=1,2, \cdots, n)$, 则 $\sum_{i=1}^n x_i=4 \pi$
$\text{D.}$ 若 $f(2 x)>f(x)$ 在 $(m, n)$ 上恒成立, 则 $n-m$ 的最大值为 $\frac{\pi}{3}$
已知函数 $f(x)=\ln x-a x$ 有两个零点 $x_1, x_2$ 且 $x_1 < x_2$, 则下列结论正确的是
$\text{A.}$ $1 < x_1 < e$
$\text{B.}$ $f(x)$ 在区间 $(e,+\infty)$ 上单调递减
$\text{C.}$ $x_1+x_2>2 e$
$\text{D.}$ 若 $a \in\left(\frac{2}{e^2}, \frac{1}{e}\right)$, 则 $x_2-x_1 < \frac{2}{a}-1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知数列 $\left\{a_n\right\}$ 为等比数列, 其前 $n$ 项和为 $S_n$, 前三项和为 13 , 前三项积为 27 , 则 $S_5=$
已知 $O$ 为 $\triangle \mathrm{ABC}$ 的外心, $A C=3, B C=4$, 则 $\overrightarrow{O C} \cdot \overrightarrow{A B}=$
已知双曲线 $\frac{x^2}{4}-\frac{y^2}{12}=1$, 过双曲线的右焦点 $F$ 作一条渐近线的平行线 $l$ 与双曲线交于点 $P$, 与另一条渐近线交于点 $Q, O$ 是坐标原点, 则 $\frac{S_{\triangle O P Q}}{S_{\triangle O P F}}=$
若存在 $a>0, b>0$, 满足 $a+t(b-2 e a) \ln b=t(b-2 e a) \ln a$, 其中 $e$ 为自然对数的底数, 则实数 $t$ 的取值范围是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
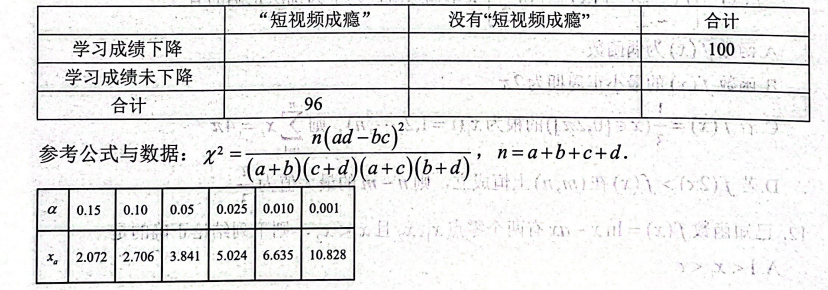
近期, 孩子刷短视频上瘾成为了家长们头疼的新问题. 某市多所中学针对此展开的一 项调查发现, 近九成学生有使用短视频平台的习惯, 近一半家长表示孩子或多或少存在 沉迷短视频的现象, 超半数家长认为短视频成瘜对青少年成长存在严重影响. 某校为调 查学生成绩下降与 “短视频成㾰” 之间是否有关随机调查了 200 名学生的开学考试成绩, 其中 “短视频成瘾” 的学生中成绩末下降的有 35 名学生. (将总排名下降 $5 \%$ 视为成绩下 降, 将刷短视频一天超过两小时规定为 “短视频成癔”)
(1)若样本中 “短视频成瘜” 且成绩末下降的女生有 15 名, 并在被认为 “短视频成瘾” 且成绩末下降的对象中按性别采用分层抽样抽取 7 人, 再从中随机抽取 2 人, 求抽到的两 人均为女生的概率.
(2) 填写下面的 $2 \times 2$ 列联表, 试根据小概率值 $\alpha=0.001$ 的独立性检验, 能否认为成 绩下降与 “短视频成癔” 有关?
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 满足 $\sqrt{3}(a \cos C+c \cos A)=2 b \sin B$, 且 $c>b$.
(1)求角 $B$;
(2) 若 $b=\sqrt{3}$, 求 $\triangle A B C$ 周长的取值范围.
如图, 三棱雉 $A-B C D$ 中, $A B=A D, A O \perp$ 平面 $B C D$, 点 $O$ 在线段 $C D$ 上, 且满足 $O D=2 O C=2, B D=\sqrt{3} O B$.
(1) 证明: $B C \perp A D$;
(2) 若二面角 $C-A B-D$ 的正弦值为 $\frac{2 \sqrt{6}}{5}$, 求三棱雉 $A-B C D$ 的体积.

已知函数 $f(x)$ 满足 $f(x)+f(1-x)=2$, 若数列 $\left\{a_n\right\}$ 满足: $a_n=f(0)+f\left(\frac{1}{n}\right)+\cdots+f\left(\frac{n-1}{n}\right)+f(1)$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若数列 $\left\{b_n\right\}$ 满足 $b_1=\frac{2}{3}, b_n=\frac{1}{a_n \cdot a_{n+1}}(n \geq 2)$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $S_n$. 若 $S_n < \lambda a_{n+1}$ 对一切 $n \in N^*$ 恒成立, 求实数 $\lambda$ 的取值范围.
已知抛物线 $C: x^2=2 p y(p>0)$, 点 $A(4,-1), P$ 为抛物线上的动点, 直线 $l$ 为抛物线的 准线, 点 $P$ 到直线 $l$ 的距离为 $d,|P A|+d$ 的最小值为 5 .
(1) 求抛物线 $C$ 的方程;
(2) 直线 $y=k x+1$ 与拋物线相交于 $M, N$ 两点, 与 $y$ 轴相交于 $Q$ 点, 当直线 $A M, A N$ 的斜率存在, 设直线 $A M, A N, A Q$ 的斜率分别为 $k_1, k_2, k_3$ 是否存在实数 $\lambda$, 使得 $\frac{1}{k_1}+\frac{1}{k_2}=\frac{\lambda}{k_3}$, 若存在, 求出 $\lambda$; 若不存在, 说明理由.
已知函数 $f(x)=e^x-a x, a \in R$.
(1) 求 $f(x)$ 的极值;
(2) 令 $F(x)=f(x)+a x+\sin x-b x-1$, 当 $1 \leq b < 2$ 时, 讨论 $F(x)$ 零点的个数.