一、单选题 (共 9 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设 $\boldsymbol{A}$ 为三阶矩阵, $\boldsymbol{P}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)$ 为可逆矩阵, 使得 $\boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P}=\left(\begin{array}{llll}1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 2\end{array}\right)$, 则 $\boldsymbol{A}^2\left(\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_2+\right.$ $\left.\boldsymbol{\alpha}_3\right)$ 是
$\text{A.}$ $\boldsymbol{\alpha}_1+2 \boldsymbol{\alpha}_3$
$\text{B.}$ $\boldsymbol{\alpha}_2+2 \boldsymbol{\alpha}_3$
$\text{C.}$ $\boldsymbol{\alpha}_1+4 \boldsymbol{\alpha}_3$
$\text{D.}$ $\boldsymbol{\alpha}_2+4 \boldsymbol{\alpha}_3$
$n$ 阶方阵 $A$ 能与对角阵相似的充分必要条件是
$\text{A.}$ $A$ 是实对称矩阵
$\text{B.}$ $A$ 的 $n$ 个特征值互不相等
$\text{C.}$ $A$ 具有 $n$ 个线性无关的特征向量
$\text{D.}$ $ A$ 的特征向量两两正交
设向量组 $\alpha_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$ 线性无关, 则下列向量组线性无关的是
$\text{A.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, \alpha_3-\alpha_1$
$\text{B.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, \alpha_1+\alpha_2+\alpha_3$
$\text{C.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, \alpha_1+2 \alpha_2+\alpha_3$
$\text{D.}$ $\alpha_1-\alpha_2, \alpha_2-\alpha_3, \alpha_3-\alpha_1$
设含有 $m$ 个方程的 $n$ 元非齐次线性方程组 $\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}$ 且 $\mathrm{r}(\boldsymbol{A})=r$, 则
$\text{A.}$ $r=n$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有解
$\text{B.}$ $r=m$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有惟一解
$\text{C.}$ $m=n$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有惟一解
$\text{D.}$ $r=m$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有解
设含有 $m$ 个方程的 $n$ 元非齐次线性方程组 $\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}$ 的系数矩阵 $\boldsymbol{A}$ 的秩为 $r$, 则
$\text{A.}$ $r=n$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有惟一解
$\text{B.}$ $m=n$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有惟一解
$\text{C.}$ $r < n$ 时, $\boldsymbol{A x}=\boldsymbol{b}$ 有无穷多解
$\text{D.}$ $r=m$ 时, $\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}$ 有解
已知三维向量 $\alpha_1=\left[\begin{array}{l}a_1 \\ a_2 \\ a_3\end{array}\right], \alpha_2=\left[\begin{array}{l}b_1 \\ b_2 \\ b_3\end{array}\right], \alpha_3=\left[\begin{array}{c}c_1 \\ c_2 \\ c_3\end{array}\right]$, 则三条直 线 $\left\{\begin{array}{l}l_1: a_1 x+b_1 y=c_1 \\ l_2: a_2 x+b_2 y=c_2 \\ l_3: a_3 x+b_3 y=c_3\end{array}\right.$ (其中 $a_i^2+b_i^2 \neq 0, i=1,2,3$ )交于 一点的充要条件是
$\text{A.}$ $\alpha_1, \alpha_2, \alpha_3$ 线性相关
$\text{B.}$ $\alpha_1, \alpha_2, \alpha_3$ 线性无关
$\text{C.}$ $r\left(\alpha_1, \alpha_2\right)=r\left(\alpha_1, \alpha_2, \alpha_3\right)$
$\text{D.}$ $\alpha_1, \alpha_2$ 线性无关, $\alpha_1, \alpha_2, \alpha_3$ 线性相关
设 $\boldsymbol{A}, \boldsymbol{B}$ 为 3 阶方阵, $\boldsymbol{A x}=0$ 有非零解, $\boldsymbol{B} \neq \boldsymbol{O}, \operatorname{tr}(\boldsymbol{A})=1$, 且 $\boldsymbol{A B}+\boldsymbol{B}=\boldsymbol{O}$, 则与 $(\boldsymbol{A}-\boldsymbol{E})^{\cdot}$ 相 似的对角矩阵为
$\text{A.}$ $\left(\begin{array}{ccc}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 2\end{array}\right)$
$\text{B.}$ $\left(\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 1\end{array}\right)$
$\text{C.}$ $\left(\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 2\end{array}\right)$
$\text{D.}$ $\left(\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{array}\right)$
设 $\mathbf{A}$ 是 $5 \times 6$ 矩阵, 而且 $\mathbf{A}$ 的行向量线性无关, 则
$\text{A.}$ $\mathbf{A}$ 的列向量线性无关;
$\text{B.}$ 线性方程组 $\mathbf{A} \mathbf{X}=\mathbf{B}$ 的增广矩阵 $\overline{\mathbf{A}}$ 的行向量线性无关;
$\text{C.}$ 线性方程组 $\mathbf{A} \mathbf{X}=\mathbf{B}$ 的增广矩阵 $\overline{\mathbf{A}}$ 的任意四个列向量线性无关;
$\text{D.}$ 线性方程组 $\mathbf{A X}=\mathbf{B}$ 有唯一解.
三元一次方程组
$$
\left\{\begin{array}{l}
x_1+x_2+a x_3=4 \\
x_1-x_2+2 x_3=-4 \\
-x_1+a x_2+x_3=a^2
\end{array}\right.
$$
所代表的三平面不可能的位置关系为
$\text{A.}$  $\text{B.}$
$\text{B.}$ 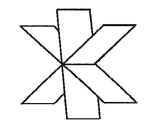 $\text{C.}$
$\text{C.}$ 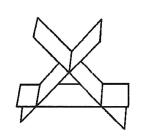 $\text{D.}$
$\text{D.}$ 
二、填空题 (共 6 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设 $\boldsymbol{\alpha}_1=(0,2,1)^{\mathrm{T}}, \quad \boldsymbol{\alpha}_2=(1,3,2)^{\mathrm{T}}, \quad \boldsymbol{\alpha}_3=(0,-1,-1)^{\mathrm{T}}$ 和 $\boldsymbol{\beta}_1=(-1,0,1)^{\mathrm{T}}, \quad \boldsymbol{\beta}_2=(1,0,0)^{\mathrm{T}}$, $\boldsymbol{\beta}_3=(-1,1,-1)^{\mathrm{T}}$ 都是 $\mathbf{R}^3$ 的基, 则 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$ 到 $\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3$ 的过渡矩阵是
若 $\boldsymbol{\eta}_1, \boldsymbol{\eta}_2, \ldots, \boldsymbol{\eta}_s$ 是非齐次线性方程组 $\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}$ 的一组解向量, 且 $k_1 \boldsymbol{\eta}_1+k_2 \boldsymbol{\eta}_2+\cdots+k_t \boldsymbol{\eta}_s$ 为导出齐次线性方程组 $A x=0$ 的解向量, 则 $k_1+k_2+\ldots+k_s=$.
$$
\text { 设 } \alpha_1=(1,2,-1,0)^{\mathrm{T}}, \alpha_2=(1,1,0,2)^{\mathrm{T}}, \alpha_3=(2,1,1, a)^{\mathrm{T}} \text { , }
$$
若向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性相关, 则 $a=$
设 $\boldsymbol{A}$ 为 3 阶矩阵, 其特征值为 $2,2,-1$, 对应的线性无关的特征向量为 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$, 令 $\boldsymbol{P}=\left(\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_3, \boldsymbol{\alpha}_2-2 \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_3\right)$, 则 $\boldsymbol{P}^{-1}\left(\boldsymbol{A}^{\cdot}+\boldsymbol{E}\right) \boldsymbol{P}=$
若向量 $\beta=(1,2, k)$ 可由向量组 $a_1=(-1,2,7), a_2=(2,1,1), a_3=(1,-1,-4)$ 线性表 示, 则 $k=$.
若向量组 $\alpha_1=(1,1,0), \alpha_2=(1,3,-1), \alpha_3=(5,3, t)$ 线性 相关,则 $t=$
三、解答题 ( 共 15 题,满分 80 分,解答过程应写出必要的文字说明、证明过程或演算步骤 )
设二次型 $f\left(x_1, x_2, x_3\right)=2 x_1^2+3 x_2^2+3 x_3^2+4 x_2 x_3$, 利用正交变换法, 把二次型 $f$ 化为标准形, 并写出正交阵。
设向量组 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m$ 线性相关, 证明: 该向量组中至少有一个向量能由其余向量线性表示.
设 $\mathrm{n}$ 阶矩阵 $A=\left(\alpha_1, \alpha_2, \cdots, \alpha_{n-1}, \alpha_n\right)$ 的前 $n-1$ 个列向量线性相关, 后 $n-1$ 个列 向量线性无关, $\beta=\alpha_1+\alpha_2+\cdots+\alpha_n$, (I) 证明: 方程组 $A x=\beta$ 必有无穷多个解; (II) 若 $\left(k_1, \cdots, k_n\right)^T$ 是 $A x=\beta$ 的任意一个解, 则必有 $k_n=1$.
$\alpha_1=\left(\begin{array}{r}2 \\ 2 \\ -1\end{array}\right), \alpha_2=\left(\begin{array}{l}0 \\ 4 \\ 8\end{array}\right), \alpha_3=\left(\begin{array}{r}-1 \\ a \\ 3\end{array}\right), \beta=\left(\begin{array}{l}1 \\ 1 \\ 2\end{array}\right), \beta$ 不能由 $\alpha_1, \alpha_2, \alpha_3$ 线性表示, 求 $a$ 的值.
已知向量组: $\alpha_1=\left(\begin{array}{r}1 \\ -1 \\ 2 \\ 4\end{array}\right), \alpha_2=\left(\begin{array}{l}0 \\ 3 \\ 1 \\ 2\end{array}\right), \alpha_3=\left(\begin{array}{r}3 \\ 0 \\ 7 \\ 14\end{array}\right), \alpha_4=\left(\begin{array}{r}1 \\ -2 \\ 2 \\ 0\end{array}\right), \alpha_5=\left(\begin{array}{r}2 \\ 1 \\ 5 \\ 10\end{array}\right)$, 求该向量组的秩和一个最大无关组, 并把其余向量用最大无关组线性表示.
设向量组: $\alpha_1=\left[\begin{array}{c}-9 \\ 1 \\ 1 \\ 1\end{array}\right], \alpha_2=\left[\begin{array}{c}2 \\ -8 \\ 2 \\ 2\end{array}\right], \alpha_3=\left[\begin{array}{c}3 \\ 3 \\ -7 \\ 3\end{array}\right], \alpha_4=\left[\begin{array}{c}4 \\ 4 \\ 4 \\ -6\end{array}\right]$, 求此向量组的秩和一个极大线性无关组, 并将其余的向量用该 极大线性无关组表示.
设向量组 $\alpha_1=(1,2,1,3)^T, \alpha_2=(4,-1,-5,-6)^T, \alpha_3=(1,-3,-4,-7)^T, \alpha_4=$ $(2,1,-1,0)^T$. 求该向量组的秩和极大无关组, 并把其余列向量用极大无关组线性表示.
设有线性方程组 $\left\{\begin{array}{l}x_1+3 x_2+x_3=0 \\ 3 x_1+2 x_2+3 x_3=-1 \\ -x_1+4 x_2+a x_3=b\end{array}\right.$, 问 $a, b$ 为何值时方程组有无穷多解? 并用基础解 系表示该通解.
设向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性无关, 证明 $\alpha_1+2 \alpha_2, 2 \alpha_2+3 \alpha_3, 3 \alpha_3+\alpha_1$ 也线性无关.
设 $\lambda_0$ 是 $n$ 阶矩阵 $A$ 的单特征值, 求证: 矩阵 $A$ 的属于特征值 $\lambda_0$ 的线 性无关的特征向量的个数恰为 1 个.
已知 $\boldsymbol{\alpha}_1=(1,1,-1,-1), \boldsymbol{\alpha}_2=(1,2,0,3)$, 求 $\boldsymbol{\alpha}_3, \boldsymbol{\alpha}_4$, 使得 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_4$ 线性无关.
设向量组 $a_1, a_2, \cdots, a_s(s>1)$ 是齐次方程组 $A \boldsymbol{X}=0$ 的一个基础解系, 证明:
$
\beta_1=a_2+a_3+\cdots+a_s, \beta_2=a_1+a_3+\cdots+a_s, \cdots, \beta_s=a_1+a_2+\cdots+a_{s-1}
$
也是该方程组的一个基础解系。
若 $\alpha, \beta, \gamma$ 线性无关, $\alpha+2 \beta, 2 \beta+k \gamma, \beta+3 \gamma$ 线性相 关,求 $k$.
求向量组
$$
\alpha_1=\left(\begin{array}{c}
1 \\
-1 \\
2 \\
4
\end{array}\right), \alpha_2=\left(\begin{array}{l}
0 \\
3 \\
1 \\
2
\end{array}\right), \alpha_3=\left(\begin{array}{c}
3 \\
0 \\
7 \\
14
\end{array}\right), \alpha_4=\left(\begin{array}{c}
1 \\
-1 \\
2 \\
0
\end{array}\right)
$$
的一个最大无关组,并将其余向量用这一最大无关组表示.
设 $a_1=[2,1,4,3]^T, a_2=[-1,1-6,6]^T, a_3=[-1,-2, a+1,-9]^T, a_4=[a, 1,-2,7]^T$, $a_5=[2,4,4,3 a+6]^T$, 若向量组的秩为 3 , 试找出一个极大无关组, 并将其他的向量用该极 大无关组线性表示。