微积分的创立是数学发展中的里程碑, 它的发展和广泛应用开创了向近代数学过渡的新时期, 为研究变量和函数提供了重要的方法和手段. 对于函数 $f(x)=\frac{1}{x}(x>0), f(x)$ 在区间 $[a, b]$ 上的图像连续不断, 从几何上看, 定积分 $\int_a^b \frac{1}{x} d x$ 便是由直线 $x=a, x=b, y=0$ 和曲线 $y=\frac{1}{x}$ 所围成的区域 (称为曲边梯形 $A B Q P)$ 的面积, 根据微积分基本定理可得 $\int_a^b \frac{1}{x} d x=\ln b-\ln a$, 因为曲边梯形 $A B Q P$ 的面积小于梯形 $A B Q P$ 的面积, 即 $S_{\text {曲边梯形 } A B Q P} < S_{\text {梯形 } A B Q P}$, 代入数据, 进一步可以推导出不等式: $\frac{a-b}{\ln ^{a-} \ln ^b}>\frac{2}{\frac{1}{a}+\frac{1}{b}}$.

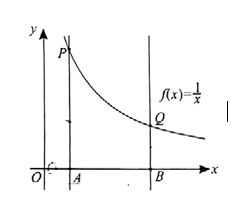
(1)请仿照这种根据面积关系证明不等式的方法, 证明: $\frac{a-b}{\ln ^{a-} \ln ^b b} < \frac{a+b}{2}$;
(2)已知函数 $g^{\prime}(x)=-2 \sin 2 x+a \cos x=-4 \sin x \cos x+a \cos x$, 其中 $a, b \in R$.
①证明: 对任意两个不相等的正数 $x_1, x_2$, 曲线 $y=f(x)$ 在 $\left(x_1, f\left(x_1\right)\right)$ 和 $\left(x_2, f\left(x_2\right)\right)$ 处的切线均不重合;
②当 $b=-1$ 时, 若不等式 $f(x) \geq 2 \sin (x-1)$ 恒成立, 求实数 $a$ 的取值范围.

如果函数 $F(x)$ 的导数 $F^{\prime}(x)=f(x)$, 可记为 $F(x)=\int f(x) d x$. 若 $f(x) \geq 0$, 则 $\int_a^b f(x) d x=F(b)-F(a)$ 表示曲线 $y=f(x)$, 直线 $x=a, x=b$ 以及 $x$ 轴围成的“曲边梯形”的面积.
(1)若 $F(x)=\int \frac{1}{x} d x$, 且 $F(1)=1$, 求 $F(x)$;
(2)已知 $0 < \alpha < \frac{\pi}{2}$, 证明: $\alpha \cos ^\alpha < \int_0^a \cos ^x d x < \alpha$, 并解释其几何意义;
(3)证明: $\frac{1}{n}\left(\sqrt{1+\cos \frac{\pi}{n}}+\sqrt{1+\cos \frac{2 \pi}{n}}+\sqrt{1+\cos \frac{3 \pi}{n}}+\cdots+\sqrt{1+\cos \frac{n \pi}{n}}\right) < \frac{2 \sqrt{2}}{\pi}, n \in N^*$.

多元导数在微积分学中有重要的应用. 设 $y$ 是由 $a, b, c \ldots$ 等多个自变量唯一确定的因变量, 则当 $a$ 变化为 $a+\Delta a$ 时, $y$ 变化为 $y+\Delta y$, 记 $\lim _{\Delta a \rightarrow 0} \frac{\Delta y}{\Delta a}$ 为 $y$ 对 $a$ 的导数, 其符号为 $\frac{\mathrm{d} y}{\mathrm{~d} a}$. 和一般导数一样, 若在 $\left(a_1, a_2\right)$ 上, 已知 $\frac{\mathrm{d} y}{\mathrm{~d} a}>0$, 则 $y$ 随着 $a$ 的增大而增大; 反之, 已知 $\frac{\mathrm{d} y}{\mathrm{~d} a} < 0$, 则 $y$ 随着 $a$ 的增大而减小.多元导数除满足一般分式的运算性质外，还具有下列性质：(1)可加性: $\frac{d\left(y_1+y_2\right)}{d a}=\frac{d y_1}{d a}+\frac{d y_2}{d a}$;
(2)乘法法则: $\frac{d\left(y_1 y_2\right)}{d a}=y_2 \frac{d y_1}{d a}+$ $y_1 \frac{d y_2}{d a}$; (3)除法法则: $\frac{d\left(\frac{y_1}{y_2}\right)}{d a}=\frac{\left(y_2 \frac{d y_1}{d a}-y_1 \frac{d y_2}{d a}\right)}{y_2^2}$; (4)复合法则: $\frac{\mathrm{d} y_2}{\mathrm{~d} a}=\frac{\mathrm{d} y_2}{\mathrm{~d} y_1} \cdot \frac{\mathrm{d} y_1}{\mathrm{~d} a}$. 记 $y=e^x+\frac{1}{e^2 \ln x \frac{1}{2 e^2 e x}}$.
( $e=2.7182818 \cdots$ 为自然对数的底数),
(1)写出 $\frac{d y}{d x}$ 和 $\frac{\mathrm{d} y}{\mathrm{~d} a}$ 的表达式;
(2) 已知方程 $y=0$ 有两实根 $x_1, x_2, x_1 < x_2$.
①求出 $a$ 的取值范围;
②证明 $\frac{d\left(x_1+x_2\right)}{d a}>0$, 并写出 $x_1+x_2$ 随 $a$ 的变化趋势.

关于 $x$ 的函数 $f(x)=\ln x+2 x-b(b>2)$, 我们曾在必修一中学习过 “二分法” 求其零点近似值. 现结合导函数,介绍另一种求零点近似值的方法——“牛顿切线法”.
(1)证明: $f(x)$ 有唯一零点 $a$, 且 $a \in(1, b)$;
(2)现在, 我们任取 $x_1 \in(1, a)$ 开始, 实施如下步骤:

在 $\left(x_1, f\left(x_1\right)\right)$ 处作曲线 $f(x)$ 的切线, 交 $x$ 轴于点 $\left(x_2, 0\right)$;
在 $\left(x_2, f\left(x_2\right)\right)$ 处作曲线 $f(x)$ 的切线, 交 $x$ 轴于点 $\left(x_3, 0\right)$;

在 $\left(x_n, f\left(x_n\right)\right)$ 处作曲线 $f(x)$ 的切线, 交 $x$ 轴于点 $\left(x_{n+1}, 0\right)$;
可以得到一个数列 $\left\{x_n\right\}$, 它的各项都是 $f(x)$ 不同程度的零点近似值.
（i）设 $x_{n+1}=g\left(x_n\right)$ ，求 $g\left(x_n\right)$ 的解析式(用 $x_n$ 表示 $x_{n+1}$ );
（ii）证明: 当 $x_1 \in(1, a)$, 总有 $x_n < x_{n+1} < a$.

在几何学常常需要考虑曲线的弯曲程度, 为此我们需要刻画曲线的弯曲程度. 考察如图所示的光滑曲线 $C: y=f(x)$ 上的曲线段 $\overparen{A B}$, 其弧长为 $\Delta s$, 当动点从 $A$ 沿曲线段 $\overparen{A B}$ 运动到 $B$ 点时, $A$ 点的切线 $l_A$ 也随着转动到 $B$ 点的切线 $l_B$, 记这两条切线之间的夹角为 $\Delta \theta$ (它等于 $l_B$ 的倾斜角与 $l_A$ 的倾斜角之差). 显然, 当弧长固定时, 夹角越大, 曲线的弯曲程度就越大; 当夹角固定时, 弧长越小则弯曲程度越大, 因此可以定义 $\bar{K}=\left|\frac{\Delta \theta}{\Delta s}\right|$ 为曲线段 $\overparen{A B}$ 的平均曲率; 显然当 $B$ 越接近 $A$, 即 $\Delta s$ 越小, $K$ 就越能精确刻画曲线 $C$ 在点 $A$ 处的弯曲程度, 因此定义 $K=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \theta}{\Delta s}\right|=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}$ (若极限存在) 为曲线 $C$ 在点 $A$ 处的曲率. (其中 $y^{\prime}, y^{\prime \prime}$ 分别表示 $y=f(x)$ 在点 $A$ 处的一阶、二阶导数）

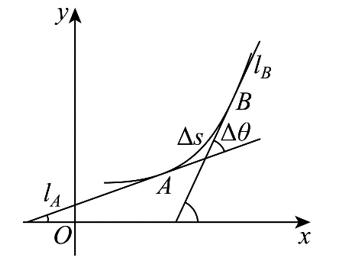
(1)求单位圆上圆心角为 $60^{\circ}$ 的圆弧的平均曲率;
(2)求椭圆 $\frac{x^2}{4}+y^2=1$ 在 $\left(\sqrt{3}, \frac{1}{2}\right)$ 处的曲率;
(3) 定义 $\varphi(y)=\frac{2 \sqrt{2}\left|y^{\prime \prime}\right|}{\left(1+y^{\prime}\right)^3}$ 为曲线 $y=f(x)$ 的“柯西曲率”. 已知在曲线 $f(x)=x \ln x-2 x$ 上存在两点 $P\left(x_1, f\left(x_1\right)\right)$和 $Q\left(x_2, f\left(x_2\right)\right)$, 且 $P, Q$ 处的“柯西曲率”相同, 求 $\sqrt[3]{x_1}+\sqrt[3]{x_2}$ 的取值范围.

同余定理是数论中的重要内容. 同余的定义为: 设 $a, b \in \mathbf{Z}, m \in \mathbf{N}_{+}$且 $m>1$. 若 $m \mid(a-b)$, 则称 $a$ 与 $b$ 关于模 $m$ 同余，记作 $a \equiv b(\bmod m)$ (“|”为整除符号).
(1)解同余方程: $x^2+2 x \equiv 0(\bmod 3)$;
(2)设（1）中方程的所有正根构成数列 $\left\{a_n\right\}$, 其中 $a_1 < a_2 < a_3 < \cdots < a_n$.
①若 $b_n=a_{n+1}-a_n\left(n \in \mathbf{N}_{+}\right)$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $S_n$, 求 $S_{4048}$ ；
②若 $C_n=\tan a_{2 n+3} \cdot \tan a_{2 n+1}\left(n \in \mathbf{N}_{+}\right)$, 求数列 $\left\{C_n\right\}$ 的前 $n$ 项和 $T_n$.

“物不知数” 是中国古代著名算题, 原载于《孙子算经》卷下第二十六题: “今有物不知其数, 三三数之剩二: 五五数之剩三; 七七数之剩二. 问物几何? ”问题的意思是, 一个数被 3 除余 2 , 被 5 除余 3 , 被 7 除余 2 , 那么这个数是多少? 若 $\mathrm{m}$ 个数 $x$ 被 $m$ 除余 $r$, 我们可以写作 $x \equiv r(\bmod m)$. 它的系统解法是秦九韶在《数书九章》大衍求一术中给出的. 大衍求一术 (也称作“中国剩余定理”) 是中国古算中最有独创性的成就之一, 现将满足上述条件的正整数从小到大依次排序. 中国剩余定理: 假设整数 $m_1, m_2, \ldots, m_n$ 两两互质, 则对任意的整数: $r_1, r_2, \ldots, r_n$ 方程组 $\left\{\begin{array}{c}x \equiv r_1\left(\bmod m_1\right) \\ x \equiv r_2\left(\bmod m_2\right) \\ \ldots \\ x \equiv r_n\left(\bmod m_n\right)\end{array}\right.$ 一定有解, 并且通解为 $x=k M+r_1 t_1 M_1+$ $r_2 t_2 M_2+\cdots+r_n t_n M_n$, 其中 $k$ 为任意整数, $M=m_1 m_2 \cdots m_n, M_i=\frac{M}{m_i}, t_i$ 为整数, 且满足 $M_i t_i=$ $1\left(\bmod m_i\right)$
(1) 求出满足条件的最小正整数, 并写出第 $n$ 个满足条件的正整数;
(2)在不超过 4200 的正整数中, 求所有满足条件的数的和. (提示: 可以用首尾进行相加).

三阶行列式是解决复杂代数运算的算法, 其运算法则如下: $\left|\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|=a_1 b_2 c_3+a_2 b_3 c_1+a_3 b_1 c_2-$ $a_3 b_2 c_1-a_2 b_1 c_3-a_1 b_3 c_2$. 若 $\vec{a} \times \vec{b}=\left|\begin{array}{ccc}\vec{\imath} & \vec{\jmath} & \vec{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2\end{array}\right|$, 则称 $\vec{a} \times \vec{b}$ 为空间向量 $\vec{a}$ 与 $\vec{b}$ 的叉乘, 其中 $\vec{a}=x_1 \vec{\imath}+$ $y_1 \vec{\jmath}+z_1 \vec{k}\left(x_1, y_1, z_1 \in R\right), \vec{b}=x_2 \vec{\imath}+y_2 \vec{\jmath}+z_2 \vec{k}\left(x_2, y_2, z_2 \in R\right)$ ， $\{\vec{\imath}, \vec{\jmath}, \vec{k}\}$ 为单位正交基底. 以 $O$ 为坐标原点、分别以 $\vec{\imath}, \vec{\jmath}, \vec{k}$ 的方向为 $x$ 轴、 $y$ 轴、 $z$ 轴的正方向建立空间直角坐标系, 已知 $A, B$ 是空间直角坐标系中异于 $O$ 的不同两点.

(1)
①若 $A(1,2,1), B(0,-1,1)$, 求 $O A \times O B$;
②证明: $\overrightarrow{O A} \times \overrightarrow{O B}+\overrightarrow{O B} \times \overrightarrow{O A}=\overrightarrow{0}$.

(2)记 $\triangle A O B$ 的面积为 $S_{\triangle A O B}$, 证明: $S_{\triangle A O B}=\frac{1}{2}|\overrightarrow{O A} \times \overrightarrow{O B}|$.

(3)证明: $(\overrightarrow{O A} \times \overrightarrow{O B})^2$ 的几何意义表示以 $\triangle A O B$ 为底面、 $|\overrightarrow{O A} \times \overrightarrow{O B}|$ 为高的三棱椎体积的 6 倍.

已知 $A_m=\left(\begin{array}{cccc}a_{1,1} & a_{1,2} & \cdots & a_{1, m} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m, 1} & a_{m, 2} & \cdots & a_{m, m}\end{array}\right)(m \geq 2)$ 是 $m^2$ 个正整数组成的 $m$ 行 $m$ 列的数表, 当 $1 \leq i < s \leq m, 1 \leq$ $j < t \leq m$ 时, 记 $d\left(a_{i, j}, a_{s, t}\right)=\left|a_{i, j}-a_{s, j}\right|+\left|a_{s, j}-a_{s, t}\right|$. 设 $n \in \boldsymbol{N}^*$, 若 $A_m$ 满足如下两个性质:
①$a_{i, j} \in\{1,2,3 ; \cdots, n\}(i=1,2, \cdots, m ; j=1,2, \cdots, m)$;
②对任意 $k \in\{1,2,3, \cdots, n\}$, 存在 $i \in\{1,2, \cdots, m\}, j \in\{1,2, \cdots, m\}$, 使得 $a_{i, j}=k$, 则称 $A_m$ 为 $\Gamma_n$ 数表.
(1)判断 $A_3=\left(\begin{array}{lll}1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2\end{array}\right)$ 是否为 $\Gamma_3$ 数表, 并求 $d\left(a_{1,1}, a_{2,2}\right)+d\left(a_{2,2}, a_{3,3}\right)$ 的值;
(2)若 $\Gamma_2$ 数表 $A_4$ 满足 $d\left(a_{i, j}, a_{i+1, j+1}\right)=1(i=1,2,3 ; j=1,2,3)$, 求 $A_4$ 中各数之和的最小值;
(3)证明: 对任意 $\Gamma_4$ 数表 $A_{10}$, 存在 $1 \leq i < s \leq 10,1 \leq j < t \leq 10$, 使得 $d\left(a_{i, j}, a_{s, t}\right)=0$.

数值线性代数又称矩阵计算, 是计算数学的一个重要分支, 其主要研究对象包括向量和矩阵. 对于平面向量 $\vec{a}=(x, y)$, 其模定义为 $|\vec{a}|=\sqrt{x^2+y^2}$. 类似地, 对于 $n$ 行 $n$ 列的矩阵 $A_{n n}=\left(\begin{array}{ccccc}a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & \cdots & \vdots\end{array}\right)$, 其模可由向量模拓展为 $A=\left(\sum_{i=1}^n \sum_{j=1}^n a_{i j}^2\right)^{\frac{1}{2}}$ (其中 $a_{i j}$ 为矩阵中第 $\mathrm{i}$ 行第 $\mathrm{j}$ 列的数, $\sum$ 为求和符号), 记作 $A_F$, 我们称这样的矩阵模为弗罗贝尼乌斯范数, 例如对于矩阵 $A_{22}=\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right)=\left(\begin{array}{ll}2 & 4 \\ 3 & 5\end{array}\right)$, 其矩阵模 $A_F=$ $\left(\sum_{i=1}^n \sum_{j=1}^n a_{i j}^2\right)^{\frac{1}{2}}=\sqrt{2^2+4^2+3^2+5^2}=3 \sqrt{6}$. 弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.
(1) $\forall n \in N^*, n \geq 3$, 矩阵 $B_{n n}=\left(\begin{array}{ccccc}1 & 0 & 0 & \cdots & 0 \\ 0 & \sqrt{2} & 0 & \cdots & 0 \\ 0 & 0 & \sqrt{3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & 0 & \cdots & \sqrt{n}\end{array}\right)$, 求使 $B_F>3 \sqrt{5}$ 的 $n$ 的最小值.
(2) $\forall n \in \boldsymbol{N}^*, n \geq 3$, , 矩阵 $C_{n n}=$
$$
\left(\begin{array}{ccccccc}
1 & \cos \theta & \cos \theta & \cos \theta & \mathrm{L} & \cos \theta & \cos \theta \\
0 & -\sin \theta & -\sin \theta \cos \theta & -\sin \theta \cos \theta & \mathrm{L} & -\sin \theta \cos \theta & -\sin \theta \cos \theta \\
0 & 0 & \sin ^2 \theta & \sin ^2 \theta \cos \theta & \mathrm{L} & \sin ^2 \theta \cos \theta & \sin ^2 \theta \cos \theta \\
\mathrm{M} & \mathrm{M} & \mathrm{M} & \mathrm{M} & & \mathrm{M} & \mathrm{M} \\
0 & 0 & 0 & 0 & \mathrm{~L} & (-1)^{n-2} \sin ^{n-2} \theta & (-1)^{n-2} \sin ^{n-2} \theta \cos \theta \\
0 & 0 & 0 & 0 & \mathrm{~L} & 0 & (-1)^{n-1} \sin ^{n-1} \theta
\end{array}\right) \text { 求 } C_F \text {. }
$$

(3)矩阵
$$
D_{m n}=\left\{\begin{array}{l}
\ln \frac{n+2}{n+1} 00 \cdots 0 \\
\ln \left(\frac{n+1}{n}\right)^{\frac{\sqrt{2}}{2}} \ln \left(\frac{n+1}{n}\right)^{\frac{\sqrt{2}}{2}} 0 \cdots 0 \\
\ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} \ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} \ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} \cdots 0 \\
\ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} \cdots \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}}
\end{array}\right.
$$
|, 证明: $\forall n \in \boldsymbol{N}^*, n \geq 3, D_F>\sqrt{\frac{n}{3 n+9}}$.

英国数学家泰勒发现了如下公式: $e^x=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\cdots+\frac{x^n}{n !}+\cdots$ 其中 $n !=1 \times 2 \times 3 \times 4 \times \cdots \times n, e$ 为自然对数的底数, $e=2.71828 \cdots \cdots$. 以上公式称为泰勒公式.设 $f(x)=\frac{e^x-e^{-x}}{2}, g(x)=\frac{e^x+e^{-x}}{2}$, 根据以上信息,并结合高中所学的数学知识, 解决如下问题.
(1)证明: $e^x \geq 1+x$;
(2)设 $x \in(0,+\infty)$, 证明: $\frac{f(x)}{x} < g(x)$;
(3) 设 $F(x)=g(x)-a\left(1+\frac{x^2}{2}\right)$, 若 $x=0$ 是 $F(x)$ 的极小值点, 求实数 $a$ 的取值范围.

英国数学家泰勒发现了如下公式: $\sin x=x-\frac{x^3}{3 !}+\frac{x^5}{5 !}-\frac{x^7}{7 !}+\cdots$, 其中 $n !=1 \times 2 \times 3 \times 4 \times \cdots \times n$, 此公式有广泛的用途, 例如利用公式得到一些不等式: 当 $x \in\left(0, \frac{\pi}{2}\right)$ 时, $\sin x < x, \sin x>x-\frac{x^3}{3 !}, \sin {x < x-\frac{x^3}{3 !}+}$ $\frac{x^5}{5 !}, \cdots$
(1)证明: 当 $x \in\left(0, \frac{\pi}{2}\right)$ 时, $\frac{\sin x}{x}>\frac{1}{2}$;
(2)设 $f(x)=m {\sin ^x} x$, 若区间 $[a, b]$ 满足当 $f(x)$ 定义域为 $[a, b]$ 时，值域也为 $[a, b]$, 则称为 $f(x)$ 的“和谐区间”.
（i） $m=1$ 时， $f(x)$ 是否存在“和谐区间”? 若存在, 求出 $f(x)$ 的所有“和谐区间”, 若不存在, 请说明理由;
（ii） $m=-2$ 时， $f(x)$ 是否存在“和谐区间”？若存在，求出 $f(x)$ 的所有“和谐区间”, 若不存在，请说明理由.

对于给定的正整数 $n$, 记集合 $R^n=\left\{\vec{\alpha} \mid \vec{\alpha}=\left(x_1, x_2, x_3, \cdots, x_n\right), x_j \in R, j=1,2,3, \cdots, n\right\}$, 其中元素 $\vec{\alpha}$ 称为一个 $n$维向量. 特别地, $\overrightarrow{0}=(0,0, \cdots, 0)$ 称为零向量. 设 $k \in R, \vec{\alpha}=\left(a_1, a_2, \cdots, a_n\right), \vec{\beta}=\left(b_1, b_2, \cdots, b_n\right) \in R^n$, 定义加法和数乘: $\vec{\alpha}+\vec{\beta}=\left(a_1+b_1, a_2+b_2, \cdots, a_n+b_n\right), k \vec{\alpha}=\left(k a_1, k a_2, \cdots, k a_n\right)$. 对一组向量 ${\alpha_1}, {\alpha_2}, \ldots, \overrightarrow{\alpha_s}$ $\left(s \in N_{+}, s \geq 2\right)$, 若存在一组不全为零的实数 $k_1, k_2, \ldots, k_s$, 使得 $k_1 \overrightarrow{\alpha_1}+k_2 \overrightarrow{\alpha_2}+\cdots+k_s \overrightarrow{\alpha_s}=\overrightarrow{0}$, 则称这组向量线性相关. 否则, 称为线性无关.
(1)对 $n=3$ ，判断下列各组向量是线性相关还是线性无关，并说明理由.
(1) $\vec{\alpha}=(1,1,1), \vec{\beta}=(2,2,2)$; (2) $\vec{\alpha}=(1,1,1), \vec{\beta}=(2,2,2), \vec{\gamma}=(5,1,4)$; (3) $\vec{\alpha}=(1,1,0), \vec{\beta}=(1,0,1), \vec{\gamma}=$ $(0,1,1), \vec{\delta}=(1,1,1)$.
(2)已知向量 $\vec{\alpha}, \vec{\beta}, \vec{\gamma}$ 线性无关, 判断向量 $\vec{\alpha}+\vec{\beta}, \vec{\beta}+\vec{\gamma}, \vec{\alpha}+\vec{\gamma}$ 是线性相关还是线性无关, 并说明理由.

(3)已知 $m(m \geq 2)$ 个向量 $ {\alpha_1}, {\alpha_2}, \ldots, \stackrel{\mathbf{u m}}{\alpha_m}$ 线性相关, 但其中任意 $m-1$ 个都线性无关, 证明下列结论:

①如果存在等式 $k_1 \overrightarrow{\alpha_1}+k_2 \overrightarrow{\alpha_2}+\cdots+k_m \overrightarrow{\alpha_m}=\overrightarrow{0}\left(k_i \in R, i=1,2,3, \cdots, m\right)$, 则这些系数 $k_1, k_2, \ldots, k_m$ 或者全为零, 或者全不为零;
②如果两个等式 $k_1 \overrightarrow{\alpha_1}+k_2 \overrightarrow{\alpha_2}+\cdots+k_m \overrightarrow{\alpha_m}=\overrightarrow{0}, l_1 \overrightarrow{\alpha_1}+l_2 \overrightarrow{\alpha_2}+\cdots+l_m \overrightarrow{\alpha_m}=\overrightarrow{0}\left(k_i \in R, l_1 \in R, i=1,2,3, \cdots\right.$ , $m$ ) 同时成立, 其中 $l_1 \neq 0$, 则 $\frac{k_1}{l_1}=\frac{k_2}{l_2}=\cdots=\frac{k_m}{l_m}$.

我们把 $a_0+a_1 x+a_2 x^2+\cdots \cdots+a_n x^n=0$ (其中 $a_n \neq 0, n \in \boldsymbol{N}^*$ ）称为一元 $n$ 次多项式方程. 代数基本定理: 任何复系数一元 $n\left(n \in N^*\right)$ 次多项式方程 (即 $a_0, a_1, a_2, \ldots, a_n$ 为实数) 在复数集内至少有一个复数根; 由此推得, 任何复系数一元 $n\left(n \in N^*\right)$ 次多项式方程在复数集内有且仅有 $n$ 个复数根（重根按重数计算). 那么我们由代数基本定理可知: 任何复系数一元 $n\left(n \in N^*\right)$ 次多项式在复数集内一定可以分解因式,转化为 $n$ 个一元一次多项式的积. 即 $a_0+a_1 x+a_2 x^2+\cdots \cdots+a_n x^n=a_n\left(x-\alpha_1\right)^{k_1}\left(x-\alpha_2\right)^{k_2} \cdots(x-$ $\left.\alpha_m\right)^{k_m}$, 其中 $k, m \in N^*, k_1+k_2+\cdots \cdots+k_m=n, \alpha_1, \alpha_2, \ldots \ldots, \alpha_m$ 为方程 $a_0+a_1 x+a_2 x^2+\cdots \cdots+$ $a_n x^n=0$ 的根. 进一步可以推出: 在实系数范围内 (即 $a_0, a_1, a_2, \ldots, a_n$ 为实数), 方程 $a_0+a_1 x+$ $a_2 x^2+\cdots \cdots+a_n x^n=0$ 的有实数根, 则多项式 $a_0+a_1 x+a_2 x^2+\cdots \cdots+a_n x^n$ 必可分解因式. 例如: 观察可知, $x=1$ 是方程 $x^3-1=0$ 的一个根, 则 $(x-1)$ 一定是多项式 $x^3-1$ 的一个因式, 即 $x^3-1=$ $(x-1)\left(a x^2+b x+c\right)$, 由待定系数法可知, $a=b=c=1$.
(1)解方程: $x^3-2 x+1=0$;
(2)设 $f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3$, 其中 $a_0, a_1, a_2, a_3 \in R^{+}$, 且 $a_0+a_1+a_2+a_3=1$.
（i）分解因式: $x-\left(a_0+a_1 x+a_2 x^2+a_3 x^3\right)$;
(ii) 记点 $P\left(x_0, y_0\right)$ 是 $y=f(x)$ 的图象与直线 $y=x$ 在第一象限内离原点最近的交点. 求证: 当 $a_1+2 a_2+$ $3 a_3 \leq 1$ 时, $x_0=1$.

帕德近似是法国数学家亨利. 帕德发明的用有理多项式近似特定函数的方法. 给定两个正整数 $m$, $n$, 函数 $f(x)$ 在 $x=0$ 处的 $[m, n]$ 阶帕德近似定义为: $R(x)=\frac{a_0+a_1 x+\cdots+a_m x^m}{1+b_1 x+\cdots+b_n x^n}$, 且满足: $f(0)=R(0), f^{\prime}(0)=$ $R^{\prime}(0), f^{\prime \prime}(0)=R^{\prime \prime}(0), \ldots, f^{(m+n)}(0)=R^{(m+n)}(0)$. (注: $f^{\prime \prime}(x)=\left[f^{\prime}(x)\right]^{\prime}, f^{\prime \prime \prime}(x)=\left[f^{\prime \prime}(x)\right]^{\prime}$, $f^{(4)}(x)=\left[f^{\prime \prime \prime}(x)\right]^{\prime}, f^{(5)}(x)=\left[f^{(4)}(x)\right]^{\prime}, \ldots ; f^{(n)}(x)$ 为 $f^{(n-1)}(x)$ 的导数) 已知 $f(x)=\ln (x+1)$ 在 $x=0$ 处的 $[1,1]$ 阶帕德近似为 $R(x)=\frac{a x}{1+b x}$.
(1)求实数 $a, b$ 的值;
(2) 比较 $f(x)$ 与 $R(x)$ 的大小;
(3)若 $h(x)=\frac{f(x)}{R(x)}-\left(\frac{1}{2}-m\right) f(x)$ 在 $(0,+\infty)$ 上存在极值, 求 $m$ 的取值范围.

“费马点”是由十七世纪法国数学家费马提出并征解的一个问题. 该问题是: “在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小. "意大利数学家托里拆利给出了解答, 当 $\triangle A B C$ 的三个内角均小于 $120^{\circ}$ 时, 使得 $\angle A O B=\angle B O C=\angle C O A=120^{\circ}$ 的点 $O$ 即为费马点; 当 $\triangle A B C$ 有一个内角大于或等于 $120^{\circ}$ 时, 最大内角的顶点为费马点. 试用以上知识解决下面问题：已知 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为$ a, b, c$, 且 $ \cos {2 B}+\cos 2 C- \cos 2 A=1$
(1)求 $A$;
(2)若 $b c=2$, 设点 $P$ 为 $\triangle A B C$ 的费马点, 求 $\overrightarrow{P A} \cdot \overrightarrow{P B}+\overrightarrow{P B} \cdot \overrightarrow{P C}+\overrightarrow{P C} \cdot \overrightarrow{P A}$;
(3) 设点 $P$ 为 $\triangle A B C$ 的费马点, $|P B|+|P C|=t|P A|$, 求实数 $t$ 的最小值.

十七世纪至十八世纪的德国数学家莱布尼兹是世界上第一个提出二进制记数法的人, 用二进制记数只需数字 0 和 1 , 对于整数可理解为逢二进 一, 例如: 自然数 1 在二进制中就表示为 $(1)_2, 2$ 表示为 $(10)_2, 3$ 表示为 $(11)_2, 5$ 表示为 $(101)_2$, 发现若 $n \in N_{+}$可表示为二进制表达式 $\left(a_0 a_1 a_2 \cdots a_{k-1} a_k\right)_2$, 则 $n=a_0 \cdot 2^k+$ $a_1 \cdot 2^{k-1}+\cdots+a_{k-1} \cdot 2^1+a_k$, 其中 $a_0=1, a_i=0$ 或 $1(i=1,2, \cdots k)$.
(1)记 $S(n)=a_0+a_1+\cdots+a_{k-1}+a_k$, 求证: $S(8 n+3)=S(4 n+3)$;
(2)记 $I(n)$ 为整数 $n$ 的二进制表达式中的 0 的个数, 如 $I(2)=1, I(3)=0$.
(i) 求 $I(60)$;
(ii) 求 $\sum_{n=1}^{511} 2^{I(n)}$ （用数字作答）.

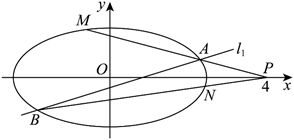
如图, 已知椭圆 $\Gamma$ 的短轴长为 4 , 焦点与双曲线 $\frac{x^2}{4-t}-\frac{y^2}{t}=1$ 的焦点重合. 点 $P(4,0)$, 斜率为 $\frac{1}{2}$ 的直线 $l_1$ 与椭圆 $\Gamma$
交于 $A, B$ 两点.
(1)求常数 $t$ 的取值范围, 并求椭圆 $\Gamma$ 的方程.
(2)(本题可以使用解析几何的方法，也可以利用下面材料所给的结论进行解答)

极点与极线是法国数学家吉拉德$\cdot$迪沙格于 1639 年在射影几何学的奠基之作《圆锥曲线论稿》中正式阐述的. 对于椭圆 $\Gamma: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 极点 $P\left(x_0, y_0\right)$ (不是原点) 对应的极线为 $l_P: \frac{x_0 x}{a^2}+\frac{y_0 y}{b^2}=1$, 且若极点 $P$ 在 $x$ 轴上, 则过点 $P$ 作椭圆的割线交 $\Gamma$ 于点 $A_1, B_1$, 则对于 $l_P$ 上任意一点 $Q$, 均有 $k_{Q A_1}+k_{Q B_1}=2 k_{P Q}$ (当斜率均存在时）.已知点 $Q$ 是直线 $l_1$ 上的一点，且点 $Q$ 的横坐标为 2. 连接 $P Q$ 交 $y$ 轴于点 $E$. 连接 $P A, P B$ 分别交椭圆 $\Gamma$ 于 $M, N$ 两点.
①设直线 $A B 、 M N$ 分别交 $y$ 轴于点 $D$ 、点 $T$, 证明: 点 $E$ 为 $D 、 T$ 的中点;
②证明直线: $M N$ 恒过定点, 并求出定点的坐标.

拓扑学是一个研究图形 (或集合) 整体结构和性质的一门几何学, 以抽象而严谨的语言将几何与集合联系起来, 富有直观和逻辑. 已知平面 $E^2=\{(x, y) \mid \forall x, y \in R\}$, 定义对 $A_1\left(x_1, y_1\right), A_2\left(x_2, y_2\right)$, 其度量 (距离) $d\left(A_1, A_2\right)=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$ 并称 $\left(E^2, d\right)$ 为一度量平面. 设 $x_0 \in\left(E^2, d\right), \varepsilon \in R^{+}$,称平面区域 $B\left(x_0, \varepsilon\right)=\left\{x \in\left(E^2, d\right) \mid d\left(x_0, x\right) < \varepsilon\right\}$ 为以 $x_0$ 为心, $\varepsilon$ 为半径的球形邻域.
(1)试用集合语言描述两个球形邻域的交集;
(2)证明: $\left(E^2, d\right)$ 中的任意两个球形邻域的交集是若干个球形邻域的并集;
(3)一个集合称作“开集”当且仅当其是一个无边界的点集. 证明： $\left(E^2, d\right)$ 的一个子集是开集当且仅当其可被表示为若干个球形邻域的并集.

随着信息技术的快速发展, 离散数学的应用越来越广泛. 差分和差分方程是描述离散变量变化的重要工
具, 并且有广泛的应用. 对于数列 $\left\{a_n\right\}$, 规定 $\left\{\Delta a_n\right\}$ 为数列 $\left\{a_n\right\}$ 的一阶差分数列, 其中 $\Delta a_n=a_{n+1}-$ $a_n\left(n \in N^*\right)$, 规定 $\left\{\Delta^2 a_n\right\}$ 为数列 $\left\{a_n\right\}$ 的二阶差分数列, 其中 $\Delta^2 a_n=\Delta a_{n+1}-\Delta a_n\left(n \in N^*\right)$.
(1)数列 $\left\{a_n\right\}$ 的通项公式为 $a_n=n^3\left(n \in \boldsymbol{N}^*\right)$, 试判断数列 $\left\{\Delta a_n\right\},\left\{\Delta^2 a_n\right\}$ 是否为等差数列, 请说明理由?求 $a$ 的值;
(3)各项均为正数的数列 $\left\{c_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $\left\{\Delta c_n\right\}$ 为常数列, 对满足 $m+n=2 t, m \neq n$ 的任意正整数 $m, n, t$ 都有 $c_m \neq c_n$, 且不等式 $S_m+S_n>\lambda S_t$ 恒成立, 求实数 $\lambda$ 的最大值.

悬链线的原理运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程. 通过适当建立坐标系, 悬链线可为双曲余弦函数 $\operatorname{ch}(x)=\frac{e^x+e^{-x}}{2}$ 的图象, 类比三角函数的三种性质: (1)平方关系: (1) $\sin ^2 x+\cos ^2 x=1$, (2)和角 $\frac{e^x-e^{-x}}{2}$.
(1)直接写出 $\operatorname{sh}(x), \operatorname{ch}(x)$ 具有的类似(1)、(2)、(3)的三种性质（不需要证明);
(2)若当 $x>0$ 时, $\operatorname{sh}(x)>a x$ 恒成立, 求实数 $a$ 的取值范围;
(3) 求 $f(x)=\operatorname{ch}(x)-\cos x-x^2$ 的最小值.

对于非空集合 $G$, 定义其在某一运算 (统称乘法) “×”下的代数结构称为“群” $(G, \times)$, 简记为 $G^{\times}$. 而判断 $G^{\times}$是否为一个群, 需验证以下三点:
1. (封闭性) 对于规定的“×”运算，对任意 $a, b \in G$ ，都须满足 $a \times b \in G$;
2. (结合律) 对于规定的“×”运算, 对任意 $a, b, c \in G$, 都须满足 $a \times(b \times c)=(a \times b) \times c$;
3. (恒等元) 存在 $e \in G$, 使得对任意 $a \in G, e \times a=a$;
4. (逆的存在性) 对任意 $a \in G$, 都存在 $b \in G$, 使得 $a \times b=b \times a=e$.

记群 $G^{\times}$所含的元素个数为 $n$, 则群 $G^{\times}$也称作“ $n$ 阶群”. 若群 $G^{\times}$的“×”运算满足交换律, 即对任意 $a, b \in$ $G, a \times b=b \times a$, 我们称 $G^{\times}$为一个阿贝尔群（或交换群）.
(1)证明：所有实数在普通加法运算下构成群 $\mathbf{R}^{+}$;并说明理由;
(2)记 $C$ 为所有模长为 1 的复数构成的集合, 请找出一个合适的“ “”运算使得 $C$ 在该运算下构成一个群 $C^{\times}$,并说明理由;
(3)所有阶数小于等于四的群 $G^{\times}$是否都是阿贝尔群? 请说明理由.

“让式子丢掉次数”: 伯努利不等式
伯努利不等式 (Bernoulli'sInequality), 又称贝努利不等式, 是高等数学的分析不等式中最常见的一种不等式, 由瑞士数学家雅各布 伯努利提出: 对实数 $x \in(-1,+\infty)$, 在 $n \in 1,+\infty)$ 时, 有不等式 $(1+x)^n \geq 1+$ $n x$ 成立; 在 $n \in(0,1)$ 时，有不等式 $(1+x)^n \leq 1+n x$ 成立.
(1)猜想伯努利不等式等号成立的条件;
(2)当 $n \geq 1$ 时, 对伯努利不等式进行证明;
(3)考虑对多个变量的不等式问题. 已知 $a_1, a_2, \cdots, a_n\left(n \in N^*\right)$ 是大于 -1 的实数（全部同号), 证明
$$
\left(1+a_1\right)\left(1+a_2\right) \cdots\left(1+a_n\right) \geq 1+a_1+a_2+\cdots+a_n
$$

交比是射影几何中最基本的不变量, 在欧氏几何中亦有应用. 设 $A, B, C, D$ 是直线 $l$ 上互异且非无穷远的四点, 则称 $\frac{A C}{B C} \cdot \frac{B D}{A D}$ (分式中各项均为有向线段长度, 例如 $A B=-B A$ ) 为 $A, B, C, D$ 四点的交比, 记为 $(A, B ; C, D)$.
(1)证明: $1-(D, B ; C, A)=\frac{1}{(B, A ; C, D)}$;
(2) 若 $l_1, l_2, l_3, l_4$ 为平面上过定点 $P$ 且互异的四条直线, $L_1, L_2$ 为不过点 $P$ 且互异的两条直线, $L_1$ 与 $l_1$, $l_2, l_3, l_4$ 的交点分别为 $A_1, B_1, C_1, D_1, L_2 与 l_1, l_2, l_3, l_4$ 的交点分别为 $A_2, B_2, C_2, D_2$, 证明: $\left(A_1, B_1 ; C_1, D_1\right)=\left(A_2, B_2 ; C_2, D_2\right)$;
(3)已知第 (2) 问的逆命题成立, 证明: 若 $\triangle E F G$ 与 $\triangle E^{\prime} F^{\prime} G^{\prime}$ 的对应边不平行, 对应顶点的连线交于同一点, 则 $\triangle E F G$ 与 $\triangle E^{\prime} F^{\prime} G^{\prime}$ 对应边的交点在一条直线上.