微积分的创立是数学发展中的里程碑, 它的发展和广泛应用开创了向近代数学过渡的新时期, 为研究变量和函数提供了重要的方法和手段. 对于函数 $f(x)=\frac{1}{x}(x>0), f(x)$ 在区间 $[a, b]$ 上的图像连续不断, 从几何上看, 定积分 $\int_a^b \frac{1}{x} d x$ 便是由直线 $x=a, x=b, y=0$ 和曲线 $y=\frac{1}{x}$ 所围成的区域 (称为曲边梯形 $A B Q P)$ 的面积, 根据微积分基本定理可得 $\int_a^b \frac{1}{x} d x=\ln b-\ln a$, 因为曲边梯形 $A B Q P$ 的面积小于梯形 $A B Q P$ 的面积, 即 $S_{\text {曲边梯形 } A B Q P} < S_{\text {梯形 } A B Q P}$, 代入数据, 进一步可以推导出不等式: $\frac{a-b}{\ln ^{a-} \ln ^b}>\frac{2}{\frac{1}{a}+\frac{1}{b}}$.

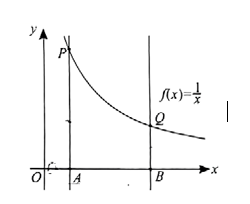
(1)请仿照这种根据面积关系证明不等式的方法, 证明: $\frac{a-b}{\ln ^{a-} \ln ^b b} < \frac{a+b}{2}$;
(2)已知函数 $g^{\prime}(x)=-2 \sin 2 x+a \cos x=-4 \sin x \cos x+a \cos x$, 其中 $a, b \in R$.
①证明: 对任意两个不相等的正数 $x_1, x_2$, 曲线 $y=f(x)$ 在 $\left(x_1, f\left(x_1\right)\right)$ 和 $\left(x_2, f\left(x_2\right)\right)$ 处的切线均不重合;
②当 $b=-1$ 时, 若不等式 $f(x) \geq 2 \sin (x-1)$ 恒成立, 求实数 $a$ 的取值范围.