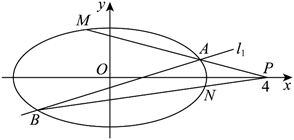
如图, 已知椭圆 $\Gamma$ 的短轴长为 4 , 焦点与双曲线 $\frac{x^2}{4-t}-\frac{y^2}{t}=1$ 的焦点重合. 点 $P(4,0)$, 斜率为 $\frac{1}{2}$ 的直线 $l_1$ 与椭圆 $\Gamma$
交于 $A, B$ 两点.
(1)求常数 $t$ 的取值范围, 并求椭圆 $\Gamma$ 的方程.
(2)(本题可以使用解析几何的方法，也可以利用下面材料所给的结论进行解答)

极点与极线是法国数学家吉拉德$\cdot$迪沙格于 1639 年在射影几何学的奠基之作《圆锥曲线论稿》中正式阐述的. 对于椭圆 $\Gamma: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 极点 $P\left(x_0, y_0\right)$ (不是原点) 对应的极线为 $l_P: \frac{x_0 x}{a^2}+\frac{y_0 y}{b^2}=1$, 且若极点 $P$ 在 $x$ 轴上, 则过点 $P$ 作椭圆的割线交 $\Gamma$ 于点 $A_1, B_1$, 则对于 $l_P$ 上任意一点 $Q$, 均有 $k_{Q A_1}+k_{Q B_1}=2 k_{P Q}$ (当斜率均存在时）.已知点 $Q$ 是直线 $l_1$ 上的一点，且点 $Q$ 的横坐标为 2. 连接 $P Q$ 交 $y$ 轴于点 $E$. 连接 $P A, P B$ 分别交椭圆 $\Gamma$ 于 $M, N$ 两点.
①设直线 $A B 、 M N$ 分别交 $y$ 轴于点 $D$ 、点 $T$, 证明: 点 $E$ 为 $D 、 T$ 的中点;
②证明直线: $M N$ 恒过定点, 并求出定点的坐标.