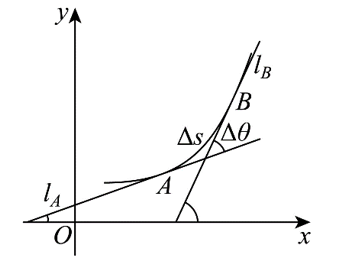
在几何学常常需要考虑曲线的弯曲程度, 为此我们需要刻画曲线的弯曲程度. 考察如图所示的光滑曲线 $C: y=f(x)$ 上的曲线段 $\overparen{A B}$, 其弧长为 $\Delta s$, 当动点从 $A$ 沿曲线段 $\overparen{A B}$ 运动到 $B$ 点时, $A$ 点的切线 $l_A$ 也随着转动到 $B$ 点的切线 $l_B$, 记这两条切线之间的夹角为 $\Delta \theta$ (它等于 $l_B$ 的倾斜角与 $l_A$ 的倾斜角之差). 显然, 当弧长固定时, 夹角越大, 曲线的弯曲程度就越大; 当夹角固定时, 弧长越小则弯曲程度越大, 因此可以定义 $\bar{K}=\left|\frac{\Delta \theta}{\Delta s}\right|$ 为曲线段 $\overparen{A B}$ 的平均曲率; 显然当 $B$ 越接近 $A$, 即 $\Delta s$ 越小, $K$ 就越能精确刻画曲线 $C$ 在点 $A$ 处的弯曲程度, 因此定义 $K=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \theta}{\Delta s}\right|=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}$ (若极限存在) 为曲线 $C$ 在点 $A$ 处的曲率. (其中 $y^{\prime}, y^{\prime \prime}$ 分别表示 $y=f(x)$ 在点 $A$ 处的一阶、二阶导数）

(1)求单位圆上圆心角为 $60^{\circ}$ 的圆弧的平均曲率;
(2)求椭圆 $\frac{x^2}{4}+y^2=1$ 在 $\left(\sqrt{3}, \frac{1}{2}\right)$ 处的曲率;
(3) 定义 $\varphi(y)=\frac{2 \sqrt{2}\left|y^{\prime \prime}\right|}{\left(1+y^{\prime}\right)^3}$ 为曲线 $y=f(x)$ 的“柯西曲率”. 已知在曲线 $f(x)=x \ln x-2 x$ 上存在两点 $P\left(x_1, f\left(x_1\right)\right)$和 $Q\left(x_2, f\left(x_2\right)\right)$, 且 $P, Q$ 处的“柯西曲率”相同, 求 $\sqrt[3]{x_1}+\sqrt[3]{x_2}$ 的取值范围.