单选题 (共 8 题 ),每题只有一个选项正确
若 $\bar{z}=\frac{2 \mathrm{i}+\mathrm{i}^2}{1+\mathrm{i}}$, 则 $z=$
$\text{A.}$ $\frac{1}{2}+\frac{3}{2} \mathrm{i}$
$\text{B.}$ $\frac{1}{2}-\frac{3}{2} \mathrm{i}$
$\text{C.}$ $-\frac{1}{2}+\frac{3}{2} \mathrm{i}$
$\text{D.}$ $-\frac{1}{2}-\frac{3}{2} \mathrm{i}$
已知全集 $U=A \cup B=\{x \in \mathbf{Z} \mid 0 < x+2 < 7\}, A=\{-1,0,1\}$, 若 $A \cap B=\varnothing$, 则 $B=$
$\text{A.}$ $\{-1,2,3,4\}$
$\text{B.}$ $\{0,1\}$
$\text{C.}$ $\{-1,0\}$
$\text{D.}$ $\{2,3,4\}$
土壤中微量元素 (如 $N, P, K$ 等) 的含量直接影响植物的生长发育, 进而影响植物群 落内植物种类的分布. 某次实验中, 为研究某微量元素对植物生长发育的具体影 响, 实验人员配比了不同浓度的溶液若干, 其浓度指标值可近似拟合为 $\mathrm{e}, \mathrm{e}, \mathrm{e}^2, \mathrm{e}^3$, $\mathrm{e}^5, \mathrm{e}^8, \mathrm{e}^{13}, \cdots$, 并记这个指标值为 $b_n$, 则 $\sum_{i=1}^{20}\left(\ln b_i\right)^2=$
$\text{A.}$ $\ln b_{19} \ln b_{20}$
$\text{B.}$ $\ln b_{20} \ln b_{21}$
$\text{C.}$ $\ln b_{19}+\ln b_{20}$
$\text{D.}$ $\ln b_{20}+\ln b_{21}$
若 $\cos \alpha-\sin \alpha=-\frac{1}{2}$, 则 $\frac{\sin \alpha \cos \alpha}{\tan ^2\left(\alpha-\frac{\pi}{4}\right)}=$
$\text{A.}$ $-\frac{21}{4}$
$\text{B.}$ $\frac{21}{4}$
$\text{C.}$ $-\frac{21}{8}$
$\text{D.}$ $\frac{21}{8}$
已知函数 $f(x)=\left\{\begin{array}{l}\frac{1}{x}-\sqrt{x}, x>0, \\ a x^2+2 a x+3, x \leqslant 0\end{array}\right.$ 有且仅有 3 个零点 $\alpha, \beta, \gamma$, 若 $\alpha < \beta < \gamma$, 则
$\text{A.}$ $\ln \alpha \beta=\gamma$
$\text{B.}$ $\ln \alpha \beta=\gamma-1$
$\text{C.}$ $\ln \alpha \beta < \gamma-1$
$\text{D.}$ $\ln \alpha \beta < \gamma$
若 $\left(\frac{1}{x}+\sqrt{x}\right)^n$ 的展开式中项的次数为整数的有且仅有 5 项, 则其常数项为
$\text{A.}$ 第 8 项
$\text{B.}$ 第7项
$\text{C.}$ 第 6 项
$\text{D.}$ 第5 项
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathbf{R}$, 且 $f(-2 x)+f(2 x)=0, f(1-2 x)-$ $f(1+2 x)=-4 x$, 则 $f(10)+f^{\prime}(11)=$
$\text{A.}$ 11
$\text{B.}$ 9
$\text{C.}$ 0
$\text{D.}$ -9
已知三棱雉 $S-A B C$ 的底面 $A B C$ 是等边三角形, 平面 $S A C \perp$ 平面 $A B C, S A=S C, \angle A S C=$ $90^{\circ}, M$ 为 $S B$ 上一点, 且 $A M \perp B C$. 设三棱雉 $S-A B C$ 外接球球心为 $O$, 则
$\text{A.}$ 直线 $O M \perp$ 平面 $S A C, O A \perp S B$
$\text{B.}$ 直线 $O M / /$ 平面 $S A C, O A \perp S B$
$\text{C.}$ 直线 $O M \perp$ 平面 $S A C$, 平面 $O A M \perp$ 平面 $S B C$
$\text{D.}$ 直线 $O M / /$ 平面 $S A C$, 平面 $O A M \perp$ 平面 $S B C$
多选题 (共 4 题 ),每题有多个选项正确
如图是函数 $f(x)=2 \sin (\omega x+\varphi)\left(\omega>0,0 < \varphi < \frac{\pi}{2}\right)$ 的部分图象, 则
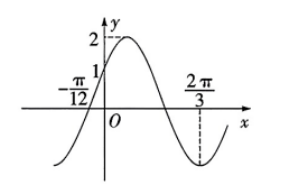
$\text{A.}$ $f(x)=2 \sin \left(2 x+\frac{\pi}{6}\right)$
$\text{B.}$ $f(x)$ 在区间 $\left[\frac{5 \pi}{6}, \frac{4 \pi}{3}\right]$ 单调递增
$\text{C.}$ 直线 $x=-\frac{\pi}{3}$ 是曲线 $y=f(x)$ 的对称轴
$\text{D.}$ $f(x)$ 的图象向左平移 $\frac{5 \pi}{12}$ 个单位得到函数 $g(x)=2 \sin 2 x$ 的图象
已知函数 $f(x)=\frac{\mathrm{e}^{|x|}}{x^2}$, 则
$\text{A.}$ $f(x)$ 为偶函数
$\text{B.}$ $f(x)$ 的最小值为 $\frac{\mathrm{e}^2}{4}$
$\text{C.}$ 函数 $g(x)=f(x)-a\left(a>\frac{\mathrm{e}^2}{4}\right)$ 有两个零点
$\text{D.}$ 直线 $\mathrm{e} x+y-2 \mathrm{e}=0$ 是曲线 $y=f(x)$ 的切线
已知 $C D$ 是圆柱 $O O_1$ 下底面圆 $O_1$ 的直径, 等腰梯形 $A B C D$ 内接于圆 $O_1$, 且 $2 A D=$ $C D=O O_1=4$, 若点 $Q$ 为上底面圆 $O$ 内 (含边界) 一点, 则
$\text{A.}$ $\triangle A B Q$ 的周长为定值
$\text{B.}$ 三棱椎 $A-B C Q$ 的体积为定值
$\text{C.}$ 三棱椎 $O-A C O_1$ 外接球的表面积为 $60 \pi$
$\text{D.}$ 直线 $A Q$ 与平面 $A C O_1$ 所成角的最小值为 $45^{\circ}$
已知直线 $y=k x+m$ 与圆 $O: x^2+y^2=4$ 交于点 $M, N$, 若过点 $M$ 和 $A(2,0)$ 的直线与 $y$ 轴交于点 $C$, 过点 $M$ 和 $B(0,2)$ 的直线与 $x$ 轴交于点 $D$, 则
$\text{A.}$ $\triangle M O N$ 面积的最大值为 2
$\text{B.}$ $\overrightarrow{M A} \cdot \overrightarrow{M B}$ 的最小值为 4
$\text{C.}$ $|A D| \cdot|B C|=8$
$\text{D.}$ 若 $k=1$, 则 $k_{O M} \cdot k_{O N}=1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
甲、乙、丙 3 名同学在《将相和》《沙家浜》《红灯记》中选择一个观看,若甲单独选 择一个剧目观看,则甲、乙、丙 3 名同学观看的剧目各不相同的概率为
在平行四边形 $A B C D$ 中, 点 $A(0,0), B(-4,4), D(2,6)$. 若 $A C$ 与 $B D$ 的交点为 $M$, 则 $D M$ 的中点 $E$ 的坐标为
已知直线 $l$ 与拋物线 $C: y^2=4 x$ 交于点 $M$, $N$, 且 $O M \perp O N$. 若 $\triangle M O N$ 的面积为 $S$, 写 出一个满足 “ $16 \leqslant S \leqslant 32$ ” 的直线 $l$ 的方程
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathbf{R}$, 且满足 $f(x)=f(-x)-2 x, x>0$ 时, $f^{\prime}(x)+1>0$. 若不等式 $f(x+\ln a)>f(x)-\ln a$ 在 $[-2,+\infty)$ 上恒成立, 则 $a$ 的取 值范围是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=2 \sqrt{3} \sin x \sin \left(\frac{\pi}{2}+x\right)-2 \cos x \sin \left(\frac{\pi}{2}-x\right)+1$.
(1) 求函数 $f(x)$ 的最值; 来源: 高三答案公众号
(2) 设 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $f(A)=2, b=2$, 且 $2 \sin B+$ $\sin C=\sqrt{7} \sin A$, 求 $\triangle A B C$ 的面积.
已知等比数列 $\left\{a_n\right\}$ 的公比为 2 , 数列 $\left\{b_n\right\}$ 满足 $b_1=2, b_2=3, a_n b_{n+1}-a_n=2^n b_n$.
(1) 求 $\left\{a_n\right\}$ 和 $\left\{b_n\right\}$ 的通项公式;
(2) 记 $S_n$ 为数列 $\left\{\frac{b_n}{a_n}\right\}$ 的前 $n$ 项和, 证明: $1 \leqslant S_n < 3$.
如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 的底面 $A B C D$ 为平行四边形, $\angle D A B=\frac{\pi}{3}, 3 A D=$ $2 C D=2 D D_1=6$, 点 $P, M$ 分别为 $A B, C D_1$ 上靠近 $A, D_1$ 的三等分点.
(1) 求点 $M$ 到直线 $P D_1$ 的距离; 来源: 高三答案公众号
(2) 求直线 $P D$ 与平面 $P C D_1$ 所成角的正弦值.

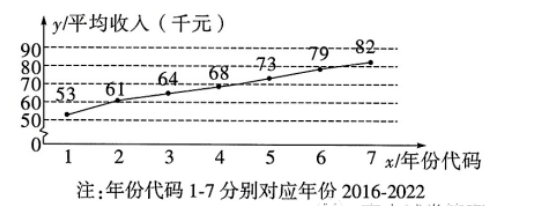
某乡政府为提高当地农民收人, 指导农民种植药材, 并在种植药材的土地附近种 草放牧, 发展畜牧业. 牛粪、羊粪等有机肥可以促进药材的生长, 发展生态循环农 业. 下图所示为某农户近 7 年种植药材的平均收人 $y$ (单位: 千元) 与年份代码 $x$ 的 折线图. 并计算得到 $\sum_{i=1}^7 y_i=480, \sum_{i=1}^7 x_i y_i=2052, $
$ \sqrt{\sum_{i=1}^7\left(y_i-\bar{y}\right)^2} \approx 25, \sum_{i=1}^7\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=$ $132, $
$\sum_{i=1}^7 w_i=140, \sum_{i=1}^7\left(w_i-\bar{w}\right)\left(y_i-\bar{y}\right)=1048, \sqrt{\sum_{i=1}^7\left(w_i-\bar{w}\right)^2} \approx 43.3$,
其中 $w_i=x_i^2$.
(1) 根据折线图判断, $y=a+b x$ 与 $y=c+d x^2$ 哪一个适宜作为平均收人 $y$ 关于年份代 码 $x$ 的回归方程类型? 并说明理由;
(2) 根据 (1) 的判断结果及数据, 建立 $y$ 关于 $x$ 的回归方程, 并预测 2023 年该农户 种植药材的平均收人;
(3)结合当地的环境和气候及对种植户的调查统计分析表明: 若继续种植现有的 药材, 农户的收人将接近 “瓶颈”. 要想继续提高农户的收人, 则需要制定新的种植 方案. 在原有的土地上继续种植原有药材, 质量得不到保障, 且影响农户经济收 人. 请先分析原因,并给出建议.
附: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$, 回归直线的斜率和截距的最小二乘法估 计公式分别为 $: b=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}, \sqrt{7} \approx 2.65$.
已知函数 $f(x)=(x-1) \mathrm{e}^x-a \ln x$.
(1) 当 $a>0$ 时,证明: $f(x)$ 存在唯一的极小值点;
(2) 若 $f(x)$ 有两个零点, 求 $a$ 的取值范围.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 点 $A$ 在 $C$ 上, 当 $A F_1 \perp x$ 轴时, $\left|A F_1\right|=\frac{1}{2}$; 当 $\left|A F_1\right|=2$ 时, $\angle F_1 A F_2=\frac{2 \pi}{3}$.
(1) 求 $C$ 的方程;
(2) 已知斜率为 -1 的直线 $l$ 与椭圆 $C$ 交于 $M, N$ 两点, 与直线 $x=1$ 交于点 $Q$, 且点 $M, N$ 在直线 $x=1$ 的两侧, 点 $P(1, t)(t>0)$. 若 $|M P| \cdot|N Q|=|M Q| \cdot|N P|$, 是否 存在到直线 $l$ 的距离 $d=\sqrt{2}$ 的 $P$ 点? 若存在, 求 $t$ 的值; 若不存在, 请说明理由.