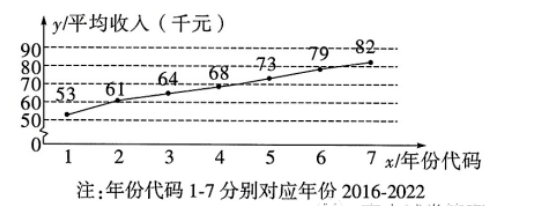
某乡政府为提高当地农民收人, 指导农民种植药材, 并在种植药材的土地附近种 草放牧, 发展畜牧业. 牛粪、羊粪等有机肥可以促进药材的生长, 发展生态循环农 业. 下图所示为某农户近 7 年种植药材的平均收人 $y$ (单位: 千元) 与年份代码 $x$ 的 折线图. 并计算得到 $\sum_{i=1}^7 y_i=480, \sum_{i=1}^7 x_i y_i=2052, $
$ \sqrt{\sum_{i=1}^7\left(y_i-\bar{y}\right)^2} \approx 25, \sum_{i=1}^7\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=$ $132, $
$\sum_{i=1}^7 w_i=140, \sum_{i=1}^7\left(w_i-\bar{w}\right)\left(y_i-\bar{y}\right)=1048, \sqrt{\sum_{i=1}^7\left(w_i-\bar{w}\right)^2} \approx 43.3$,
其中 $w_i=x_i^2$.
(1) 根据折线图判断, $y=a+b x$ 与 $y=c+d x^2$ 哪一个适宜作为平均收人 $y$ 关于年份代 码 $x$ 的回归方程类型? 并说明理由;
(2) 根据 (1) 的判断结果及数据, 建立 $y$ 关于 $x$ 的回归方程, 并预测 2023 年该农户 种植药材的平均收人;
(3)结合当地的环境和气候及对种植户的调查统计分析表明: 若继续种植现有的 药材, 农户的收人将接近 “瓶颈”. 要想继续提高农户的收人, 则需要制定新的种植 方案. 在原有的土地上继续种植原有药材, 质量得不到保障, 且影响农户经济收 人. 请先分析原因,并给出建议.
附: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$, 回归直线的斜率和截距的最小二乘法估 计公式分别为 $: b=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}, \sqrt{7} \approx 2.65$.
$ \sqrt{\sum_{i=1}^7\left(y_i-\bar{y}\right)^2} \approx 25, \sum_{i=1}^7\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=$ $132, $
$\sum_{i=1}^7 w_i=140, \sum_{i=1}^7\left(w_i-\bar{w}\right)\left(y_i-\bar{y}\right)=1048, \sqrt{\sum_{i=1}^7\left(w_i-\bar{w}\right)^2} \approx 43.3$,
其中 $w_i=x_i^2$.
(1) 根据折线图判断, $y=a+b x$ 与 $y=c+d x^2$ 哪一个适宜作为平均收人 $y$ 关于年份代 码 $x$ 的回归方程类型? 并说明理由;
(2) 根据 (1) 的判断结果及数据, 建立 $y$ 关于 $x$ 的回归方程, 并预测 2023 年该农户 种植药材的平均收人;
(3)结合当地的环境和气候及对种植户的调查统计分析表明: 若继续种植现有的 药材, 农户的收人将接近 “瓶颈”. 要想继续提高农户的收人, 则需要制定新的种植 方案. 在原有的土地上继续种植原有药材, 质量得不到保障, 且影响农户经济收 人. 请先分析原因,并给出建议.
附: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$, 回归直线的斜率和截距的最小二乘法估 计公式分别为 $: b=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}, \sqrt{7} \approx 2.65$.
