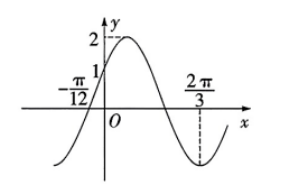
如图是函数 $f(x)=2 \sin (\omega x+\varphi)\left(\omega>0,0 < \varphi < \frac{\pi}{2}\right)$ 的部分图象, 则
$\text{A.}$ $f(x)=2 \sin \left(2 x+\frac{\pi}{6}\right)$
$\text{B.}$ $f(x)$ 在区间 $\left[\frac{5 \pi}{6}, \frac{4 \pi}{3}\right]$ 单调递增
$\text{C.}$ 直线 $x=-\frac{\pi}{3}$ 是曲线 $y=f(x)$ 的对称轴
$\text{D.}$ $f(x)$ 的图象向左平移 $\frac{5 \pi}{12}$ 个单位得到函数 $g(x)=2 \sin 2 x$ 的图象