单选题 (共 8 题 ),每题只有一个选项正确
集合 $A=\left\{x \mid y=\sqrt{x^2+x-6}\right\}, B=\left\{x \mid \frac{x-a-2}{x-a} \leq 0\right\}$, 若 $A \cap B=\{x \mid 2 \leq x \leq 3\}$, 则 $a$ 的值为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
已知复数 $\frac{x+y \mathrm{i}}{1+\mathrm{i}}=2-\mathrm{i}, x, y \in \mathrm{R}$, 则 $x-y=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
已知 $\sin \left(45^{\circ}+\alpha\right)=\frac{\sqrt{5}}{5}, 45^{\circ} < \alpha < 135^{\circ}$, 则 $\cos \alpha$ 的值为
$\text{A.}$ $\frac{3 \sqrt{10}}{10}$
$\text{B.}$ $-\frac{3 \sqrt{10}}{10}$
$\text{C.}$ $\frac{\sqrt{10}}{10}$
$\text{D.}$ $-\frac{\sqrt{10}}{10}$
恩格尔系数 $n=\frac{\text { 食品消费支出总额 }}{\text { 消费支出,总额 }} \times 100 \%$, 国际上常用恩格尔系数 $n$ 来衡量一个地
区家庭的富裕程度, 恩格尔系数越低, 人民生活越富裕. 某地区家庭 2022 年底恩格尔系 数 $n$ 为 $50 \%$, 刚达到小康, 预计从 2023 年起该地区家庭每年消费支出总额增加 $30 \%$, 食 品消费支出总额缯加 $20 \%$, 依据以上数据, 预计该地区家庭恩格尔系数 $n$ 满足 $30 \% < n \leq 40 \%$ 达到富裕水平, 至少经过 ( ) 年 (参考数据: $\lg 0.6 \approx-0.22, \lg 0.8 \approx-0.10, \lg 12 \approx 1.08$, $\lg 13 \approx 1.11)$
$\text{A.}$ 8年
$\text{B.}$ 7年
$\text{C.}$ 4年
$\text{D.}$ 3年
如图, 圆 $O$ 半径为 1 , 圆外一点 $P$ 到圆心 $O$ 的距离为 2 , 过 $P$ 引圆 $O$ 的两条切线, 切 点分别记为 $A 、 B, M$ 为圆 $O$ 上的一个动点, 则 $\overrightarrow{P A} \cdot \overrightarrow{P M}$ 的最小值为
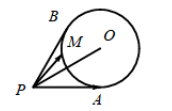
$\text{A.}$ $\sqrt{3}-1$
$\text{B.}$ $3-\sqrt{3}$
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ $\sqrt{3}$
已知双曲线 $C: \frac{x^2}{12}-\frac{y^2}{4}=1$, 点 $F$ 是 $C$ 的右焦点, 若点 $P$ 为 $C$ 左支上的动点, 设点 $P$ 到 $C$ 的一条渐近线的距离为 $d$, 则 $d+|P F|$ 的最小值为
$\text{A.}$ $2+4 \sqrt{3}$
$\text{B.}$ $6 \cdot \sqrt{3}$
$\text{C.}$ $8$
$\text{D.}$ $10$
如图 1 所示, 四边形 $A B C D$ 是边长为 2 的正方形, 点 $E 、 F 、 M$ 分别为线段 $B C$ 、 $C D 、 B E$ 的中点, 分别沿 $A E 、 A F$ 及 $E F$ 所 在直线把 $\triangle A E B, \triangle A F D$ 和 $\triangle E F C$ 折起, 使$B 、 C 、 D$ 三点重合于点 $P$, 得到如图 2 所示的三棱锥 $P-A E F$, 则下列结论中正确的有
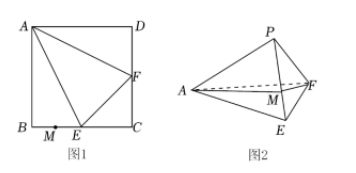
$\text{A.}$ 点 $P$ 在平面 $A E F$ 上的投影为 $\triangle A E F$ 的外心
$\text{B.}$ 直线 $A M$ 与平面 $P E F$ 所成角的正切值为 2
$\text{C.}$ 三棱锥 $P-A E F$ 的内切球半径为 $\frac{1}{2}$
$\text{D.}$ 过点 $M$ 的平面截三棱锥 $P-A E F$ 的外接球所得截面的面积的取值范围为 $\left[\frac{\pi}{4}, \frac{3 \pi}{2}\right]$
已知 $a=e^{0.2}, b=\log _7 8, c=\log _6 7$, 则
$\text{A.}$ $a > b > c$
$\text{B.}$ $b > a > c$
$\text{C.}$ $a > c > b$
$\text{D.}$ $c > a > b$
多选题 (共 4 题 ),每题有多个选项正确
如图, 在棱长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $M, N$ 分别是 $A D_1, B D_1$ 的中点, 则
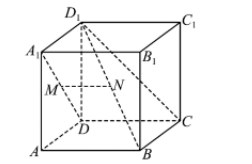
$\text{A.}$ 四点 $A_1, M, N, C$ 共面
$\text{B.}$ 直线 $A_1 D$ 与平面 $B C D_1$ 平行
$\text{C.}$ 异面直线 $C N$ 与 $D_1 C_1$ 所成角的余弦值为 $\frac{\sqrt{3}}{3}$
$\text{D.}$ 过 $M, B, C$ 三点的平面截正方体所得图形面积为 $\sqrt{5}$
已知函数 $f(x)=x^3+a x^2+b x+c(a, b, c \in R)$, 则下列说法正确的是
$\text{A.}$ 若函数 $f(x)$ 的图象关于点 $(1, f(1))$ 中心对称, 则 $a=-3$
$\text{B.}$ 当 $c=0$ 时,函数 $f(x)$ 过原点的切线有且仅有两条
$\text{C.}$ 函数 $f(x)$ 在 $[-1,1]$ 上单调递减的充要条件是 $2 a-b \geq 3$
$\text{D.}$ 若实数 $x_1, x_2$ 是 $f(x)$ 的两个不同的极值点, 且满足 $x_1+x_2=x_1 x_2$, 则 $a>0$ 或 $a < -6$
已知函数 $f(x)=2 \sin x+|\sin 2 x|$, 则
$\text{A.}$ $f(x)$ 的最小正周期为 $2 \pi$
$\text{B.}$ $f(x)$ 的图象关于 $x=\frac{\pi}{2}$ 对称
$\text{C.}$ $f(x)$ 在 $[0,2 \pi]$ 上有四个零点
$\text{D.}$ $f(x)$ 的值域为 $\left[-2, \frac{3 \sqrt{3}}{2}\right]$
已知抛物线 $C: y^2=4 x$, 过焦点 $F$ 的直线 $l$ 与 $C$ 交于 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 两点, $y_1>2$,
$E$ 与 $F$ 关于原点对称, 直线 $A B$ 与直线 $A E$ 的倾斜角分别是 $\alpha$ 与 $\beta$, 则
$\text{A.}$ $\sin \alpha>\tan \beta$
$\text{B.}$ $\angle A E F=\angle B E F$
$\text{C.}$ $\angle A E B < 90^{\circ}$
$\text{D.}$ $\alpha < 2 \beta$
填空题 (共 9 题 ),请把答案直接填写在答题纸上
$(\sqrt{2} x-y)^5$ 展开式中 $x^2 y^3$ 的系数为
已知圆 $O_1:(x-m)^2+(y+2)^2=9$ 与圆 $O_2:(x+n)^2+(y+2)^2=1$ 内切, 则 $m^2+n^2$ 的 最小值为
已知某批零件的质量指标 $\xi$ (单位:毫米)服从正态分布 $N\left(25.40, \sigma^2\right)$, 且
$P(\xi \geq 25.45)=0.1$, 现从该批雪件中随机取 3 件, 用 $X$ 表示这 3 件产品的质量指标值 $\xi$ 不
位于区间 $(25.35,25.45)$ 的产品件数, 则 $D(X)=$
已知函数 $f(x)=\left\{\begin{array}{l}(2 x-3) \mathrm{e}^x, x>0 \\ e x-a, x \leq 0\end{array}\right.$, 若 $f\left(x_1\right)=f\left(x_2\right)$, 且 $\left|x_1-x_2\right|$ 的最大值为 4 , 则 实数 $a$ 的值为
记锐角 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $\frac{\sin (A-B)}{\cos B}=\frac{\sin (A-C)}{\cos C}$.
(1) 求证: $B=C$;
(2)若 $a \sin C=2$, 求 $\frac{1}{a^2}+\frac{1}{b^2}$ 的最大值.
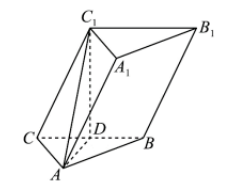
如图, 在三棱柱 $A B C-A_1 B_1 C_1$ 中, $\triangle A B C$ 为边长为 2 的
正三角形, $\mathrm{D}$ 为 $B C$ 的中点, $A A=2$, 且 $\angle C_1 C B=60^{\circ}$, 平 面 $B B_1 C_1 C \perp$ 平面 $A B C$.
(1)证明: $C_1 D \perp A B$;
(2)求二面角 $A_1-A C_1-D$ 的正弦值.
某购物中心准备进行扩大规模, 在制定末来发展策略时, 对中心的现有顾客满意度进行了一个初步的现场调查, 分别调查顾客对购物中心的商品质量、服务质量、购物环境、广告宣传的满意程度。调查时将对被抽中的每个顾客从这四个问题中随机抽取两个问题来提问, 统计顾客的满意情况。假设, 有三名顾客被抽到, 且这三名顾客对这四个问题的满意情况如下表:
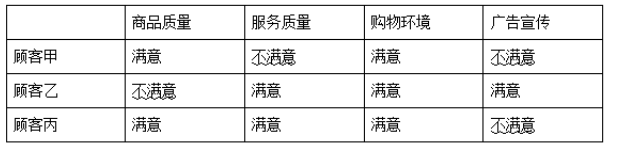
每得到一个满意加 10 分, 最终以总得分作为制定发展策略的参考依据。
(1)求购物中心得分为 50 分的概率;
(2)若已知购物中心得分为 50 分, 则顾客丙投出一个不满意的概率为多少?
(3) 列出该购物中心得到满意的个数 $\mathrm{X}$ 的分布列, 并求得分 $\xi$ 的数学期望。
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{2}}{2}$, 过点 $\left(-1, \frac{\sqrt{2}}{2}\right)$.
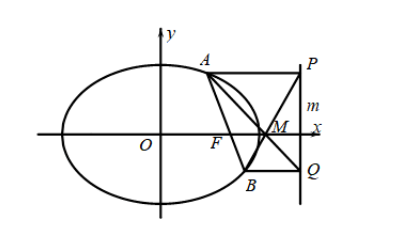
(1) 求椭圆 $C$ 的标准方程;
(2) 设椭圆的右焦点为 $F$, 定直线 $m: x=2$, 过点 $F$ 且斜率不为霝的直线 $l$ 与椭圆交于 $A$, $B$ 两点, 过 $A, B$ 两点分别作 $A P \perp m$ 于 $P, B Q \perp m$ 于 $Q$, 直线 $A Q 、 B P$ 交于点 $M$, 证明: $M$ 点为定点, 并求出 $M$ 点的坐标.
已知函数 $f(x)=e^x+2 a x-1$, 其中 $a$ 为实数, $e$ 为自然对数底数, $e=2.71828 \cdots$.
(1) 已知函数 $x \in R, f(x) \geq 0$, 求实数 $a$ 取值的集合;
(2)已知函数 $F(x)=f(x)-a x^2$ 有两个不同极值点 $x_1 、 x_2$, 证明 $2 \sqrt{a}\left(x_1+x_2\right)>3 x_1 x_2$
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在数列 $\left\{a_n\right\}$ 中, $a_1=a_2=1$, 且 $a_{n+2}+(-1)^{\prime \prime} a_n=4$.
(1)令 $b_n=a_{2 n-1}$, 证明: 数列 $\left\{b_n\right\}$ 为等差数列, 并求数列 $\left\{b_n\right\}$ 的通项公式;
(2)记数列 $\left\{a_n\right\}$ 的前 $\mathrm{n}$ 项和为 $S_n$, 求 $S_{23}$.