已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{2}}{2}$, 过点 $\left(-1, \frac{\sqrt{2}}{2}\right)$.

(1) 求椭圆 $C$ 的标准方程;
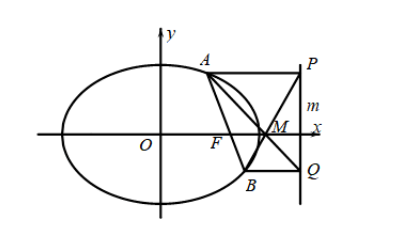
(2) 设椭圆的右焦点为 $F$, 定直线 $m: x=2$, 过点 $F$ 且斜率不为霝的直线 $l$ 与椭圆交于 $A$, $B$ 两点, 过 $A, B$ 两点分别作 $A P \perp m$ 于 $P, B Q \perp m$ 于 $Q$, 直线 $A Q 、 B P$ 交于点 $M$, 证明: $M$ 点为定点, 并求出 $M$ 点的坐标.