查看原题
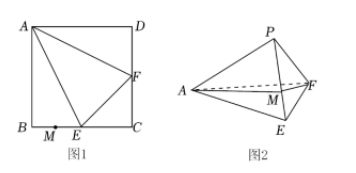
如图 1 所示, 四边形 ABCD 是边长为 2 的正方形, 点 E、F、M 分别为线段 BC 、 CD、BE 的中点, 分别沿 AE、AF 及 EF 所 在直线把 △AEB,△AFD 和 △EFC 折起, 使B、C、D 三点重合于点 P, 得到如图 2 所示的三棱锥 P−AEF, 则下列结论中正确的有
A. 点 P 在平面 AEF 上的投影为 △AEF 的外心     B. 直线 AM 与平面 PEF 所成角的正切值为 2     C. 三棱锥 P−AEF 的内切球半径为 12     D. 过点 M 的平面截三棱锥 P−AEF 的外接球所得截面的面积的取值范围为 [π4,3π2]         
不再提醒